



Next: 3.4.2 Vektorrechnung
Up: 3.4 Vektorrechnung, lineare Algebra
Previous: 3.4 Vektorrechnung, lineare Algebra
3.4.1 Matrizen
Wenn wir also eine Matrix auf unseren Schirm bringen wollen, müssen wir zuerst
einen Variablentyp Matrix deklarieren:
-
- MI:=Matrix( Integer);
definiert den Ganzzahlen-Matrixtyp MI,
-
- MR:=Matrix(Rational);
definiert den rationalen Matrixtyp MR.
Nun können wir eine Matrix3.21herstellen:
-
- A:=MR([[1,2,3],[4,5,6],[7,8,9]]);
Diese Matrix sieht nun so aus:
![\( A=\left[ \begin{array}{ccc}
1 & 2 & 3\\
4 & 5 & 6\\
7 & 8 & 9
\end{array}\right] \)](img40.gif)
Wir können aber die Typdefinition MuPAD überlassen, für Vektoren ist dies sogar
notwendig. Das Ganze wird dann einfacher. Für obiges Beispiel kann der Aufruf
nun auch so aussehen:
-
- A:=Matrix()([[1,2,3],[4,5,6],[7,8,9]]);
für einen Vektor
![\( \overrightarrow{b}=\left[ \begin{array}{c}
1\\
2\\
3
\end{array}\right] \)](img41.gif) schreibt man:
schreibt man:
-
- b:=Matrix()([[1,2,3]]);
Ok. Wir wissen nun, wie man Matrizen und Vektoren definiert. Mit dem Kommando
,,type(A);`` können wir jederzeit den Matrixtyp der Matrix A
erfahren.
Jetzt können wir die Standardfunktionen von MuPAD auf diese Matrix anwenden:
![\( A=\left[ \begin{array}{cc}
1 & 2\\
0 & -3
\end{array}\right] \)](img42.gif) ;
B=A*3; C=A-B;
;
B=A*3; C=A-B;
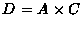
Eingabe in MuPAD:
-
- A:=mq([[1,2],[0,-3]]);
Ausgabe von MUPAD:
-
- +- -+
| 1, 2 |
| |
| 0, -3 |
+- -+
Eingabe in MuPAD:
-
- B:=3*A;
Ausgabe von MuPAD:
-
- +- -+
| 3, 6 |
| |
| 0, -9 |
+- -+
Eingabe in MuPAD:
-
- C:=A-B;
Ausgabe von MuPAD:
-
- +- -+
| -2, -4 |
| |
| 0, 6 |
+- -+
Eingabe in MuPAD:
-
- D:=A*C;
Ausgabe von MuPAD:
-
- +- -+
| -2, 8 |
| |
| 0, -18 |
+- -+
Hier eine kurze Übersicht über die Befehle zur Matrizenmanipulation:
|
Funktion |
Beschreibung |
Beispiel |
| det() |
Ermittelt die Determinante |
nur für quadrat. Matrix |
| dimen() |
Dimension der Matrix |
| eigenvalues() |
Eigenwert der Matrix |
| eigenvectors() |
Eigenwerte u. -vektoren |
| gaussElim() |
Gaussch. Elimin. |
| gaussJordan() |
Gauss-Jordan Elim. |
| grad() |
Grad der Matrix |
| jordanform() |
Jordanform |
| linearSolve() |
löst Matrix A nach Boder
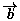 |
A,
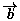 :
,,linearSolve(A, b);`` :
,,linearSolve(A, b);`` |
| rank() |
Rang der Matrix |
| sylvester() |
Sylvesterform |
| transpose() |
vertauscht Zeilen und Spalten |
quadrat. Matrix |
Da die Befehle zur Matrizenmanipulation sich in einigen MuPAD-Versionen unterscheiden,
sollte man unbedingt ,,?linalg`` eingeben und sich mit der
genauen Syntax bekannt machen.
Footnotes
- ... Matrix3.21
-
oder mehrere




Next: 3.4.2 Vektorrechnung
Up: 3.4 Vektorrechnung, lineare Algebra
Previous: 3.4 Vektorrechnung, lineare Algebra
© 1999 by Andreas Romeyke, spezielle Version als Teil der Leipzig-Kolleg Homepages
free for non-commercial usage - frei für den nichtkommerziellen Gebrauch, benötigt mindestens HTML 3.2, grafikfähigen Browser
Dokument ist auch als DVI bzw. PS in einer druckbaren Version (zB. für Lynx-Benutzer) verfügbar, sh. Startseite
![\( A=\left[ \begin{array}{cc}
1 & 2\\
0 & -3
\end{array}\right] \)](img42.gif) ;
B=A*3; C=A-B;
;
B=A*3; C=A-B;
![\( A=\left[ \begin{array}{ccc}
1 & 2 & 3\\
4 & 5 & 6\\
7 & 8 & 9
\end{array}\right] \)](img40.gif)
![\( \overrightarrow{b}=\left[ \begin{array}{c}
1\\
2\\
3
\end{array}\right] \)](img41.gif) schreibt man:
schreibt man:
![\( A=\left[ \begin{array}{cc}
1 & 2\\
0 & -3
\end{array}\right] \)](img42.gif) ;
B=A*3; C=A-B;
;
B=A*3; C=A-B;
![]()