Kryptologie - eine Einführung

Inhaltsverzeichnis



Vorwort

Dieses Dokument enstand im Rahmen eines Projektes an der FH Leipzig als "Abfallprodukt" für einen Fachbericht. Es soll diesen nicht nur ergänzen, sondern allen Interessierten einen tieferen Ein- und Überblick zu der Geschichte, den Verfahren und der Anwendung der Geheimwissenschaft Kryptologie bieten. Für die grobe Struktur und einzelnen Beiträge und Grafiken zeichneten sich verantwortlich:



Dieses Dokument in der Rohfassung entstand durch Steve Lingel, Tobias Höppner, Michael Schreiter und Andreas Romeyke. Die aktuelle Version wird gepflegt durch Andreas Romeyke. Durch die Verwendung von Tabellen und Grafiken ist es empfehlenswert auf einen Textbrowser a la lynx zu verzichten. Netscape,Mozilla, Konqueror, Opera und Co. können bedenkenlos verwendet werden, ebenso w3m als lynx-Ersatz. Es wird angestrebt in künftigen Versionen dieses Dokument html4.0 strikt konform zu gestalten und auf "font"-Tags zu verzichten und CSS1 zu verwenden. Fehlerhinweise oder Vorschläge gehen bitte an mich.

Copyright

Soweit nicht anders vermerkt, kann dieser Text unter der Gnu Public Documentation License verwendet werden. Für den genauen Wortlaut sei auf http://www.gnu.org verwiesen.

Sollten Rechte Dritter in diesem Text verletzt worden sein, bitten wir um schriftliche Benachrichtigung.

Einleitung

Zur Bedeutung der Kryptologie

Kryptologie spielt in unserer heutigen Zeit eine immer wichtiger werdende Rolle. Dies ist in dem Wandel von der Industrie- zur Informationsgesellschaft begründet. Täglich hat jeder von uns mit kryptologischen Technologien bewußt oder unbewußt zu tun. Sei es das bargeldlose Bezahlen mittels EC-Karte, das Benutzen von Kartentelefonen oder Handys, der Umgang mit Computern am Arbeitsplatz oder die Nutzung von Bezahl-Fernsehen (Pay-TV). Die Entwicklung und die Bedeutung der Kryptologie herauszustellen, sowie Anregungen für die tiefere Beschäftigung mit dieser Materie zu geben, soll das erklärte Ziel dieser Publikation sein.


Grundbegriffe

Zunächst einige Worte zur Terminologie. Die Begriffe Kryptologie und Kryptographie sind aus den griechischen Wörtern kryptos (geheim) logos (das Wort, der Sinn), und graphein (schreiben) gebildet. Meist wird mit Kryptologie die Gesamtheit der Kryptoanalyse und Kryptographie bezeichnet, wobei die Kryptographie sich mit der Verheimlichung von Nachrichten und die Kryptoanalyse mit dem Brechen von geheimen Nachrichten beschäftigt.

Ein Klartext ist die Information, die der Empfänger erhalten soll. Ein Geheimtext ist ein verschlüsselter Klartext, das heißt für Andere nicht mehr lesbar. Den Vorgang der Verschlüsselung bezeichnet man auch als Chiffrierung, den der Entschlüsselung als Dechiffrierung. Die Begriffe Chiffre oder Code bezeichnen das Verfahren, das der Chiffrierung bzw. der Dechiffrierung zugrunde liegt. Die geheime Information, die zur Verschlüsselung und Entschlüsselung dient, nennt man Schlüssel. Wird zum Chiffrieren und Dechiffrieren der gleiche Schlüssel benutzt, so spricht man von einem symmetrischem Verfahren. Dem gegenüber gibt es Verfahren, bei denen zwei oder mehr Schlüssel verwendet werden, das heißt der Chiffrierschlüssel ist ein anderer, als der Dechiffrierschlüssel. Diese Verfahren sind asymmetrisch und werden auch als public-key-Verfahren bezeichnet. Unter einem Angreifer versteht man einen unbefugten Dritten, der sich den Klartext und/oder Schlüssel beschaffen will. Ein aktiver Angriff erfolgt, wenn die verschlüsselte Nachricht abgefangen und gegen eine gefälschte Version ausgetauscht und als echt deklariert wird. Ein passiver Angriff bezeichnet den Vorgang des Abhörens bzw. das Entschlüsseln der Nachricht.


Die Kryptographie teilt sich grob in die drei Aufgabenbereiche der Geheimhaltung, Integrität und Authentizität auf, wobei sich letztere mit der Übertragungs- und Fälschungssicherheit beschäftigen.


Geschichte der Kryptologie

ca. 600 v. Chr.

In Palästina werden Texte mit der ATBASH verschlüsselt.

ca. 500 v. Chr.

Die Griechen verschlüsseln Nachrichten mit Hilfe der SKYTALE.

ca. 200 v. Chr.

Der Grieche Polybious beschreibt erstmals sein POLYBIOUS-System.

ca. 100 - 44 v. Chr.

Julius Caesar schrieb vertrauliche Botschaften in dem nach ihm benannten CAESAR-CODE.

ca. 500 - 1400 n. Chr.

in Europa beginnt die „Dunkle Zeit der Kryptographie“, d.h. sie wurde der schwarzen Magie zugeordnet, in dieser Zeit ging viel Wissen über die Kryptographie verloren, im Gegensatz dazu blühte die Kryptographie im persischen Raum auf

855 n. Chr.

Im arabischen Raum erscheint das erste Buch über Kryptologie. Abu ‘Abd al-Raham al-Khahil ibn Ahmad ibn’Amr ibn Tammam al Farahidi al-Zadi al Yahamadi beschreibt stolz in seinem Buch unter anderem die geglückte Entschlüsselung eines für den byzantinischen Kaiser bestimmten griechischen Codes

1412

eine 14-bändige arabische Enzyklopädie beschreibt auch kryptographische Methoden, dabei wird neben der Substitution und der Transposition, erstmals die Methode der mehrmaligen Substitution an einem Klartextzeichen erwähnt

1397

Auf Wusch Clemens des 7. erfindet Gabrieli di Lavinde die erste Nomenklatur (Nomenklatur-Code). Dieser Nomenklatur-Code wurde wegen seiner Einfachheit in den nächsten 450 Jahren vor allem in diplomatischen Kreisen verwendet.

1466

Leon Battista Alberti (1404 - 1472) , einer der führenden Kräfte der italienischen Renaissance, veröffentlicht sein Buch „Modus scribendi in ziferas“, indem erstmals die von ihm erfundenen Chiffrierscheiben erwähnt. Albertis zahlreiche kryptologischen Leistungen beruhen auf der Tatsache, das er Sekretär jener Behörde war, die sich an der römischen Kurie (päpstlicher Hof) mit Geheimschriften befasste. Er wird als „Vater der Kryptographie“ bezeichnet.

1518

Im deutschsprachigen Raum erscheint das erste gedruckte Buch über Kryptologie. Der Verfasser ist Johannes Trithemius.

1586

Das Buch „Tractié de Chiffre“ des französischen Diplomaten Blaise de Vigenère11 erscheint. SeineVerschlüsselungsmethode, die später nach ihm als Vigenère-Code benannt wurde, wird so der Öffentlichkeit zugänglich gemacht. Dieser Code ist der bekannteste unter allen polyalphabetischen Algorithmen.

1628

Antione Rissignol wird der erste vollzeitlich angestellte Kryptoanalytiker, nachdem seine Entschlüsselung einer feindlichen chiffrierten Botschaft die Belagerung Realmonts durch die Hugenotten beendete. Seitdem sind Kryptoanalytiker ein fester Bestandteil des militärischen Apparats.

1700

russischer Zar benutzte eine große Code-Tabelle von 2000-3000 Silben und Worten zur Chiffrierung seiner Botschaften

1795

Thomas Jefferson entwickelt den ersten Chiffrierzylinder namens „wheel cypher“. Er benutzte sie aber nie, so daß sie in Vergessenheit geriet bzw. nie der Öffentlichkeit zugänglich wurde. Somit wurde der Chiffrierzylinder parallel zu Jeffersons unbekannter Erfindung an unterschiedlichen Orten nochmals erfunden:

1854

der Engländer Charles Babbage erfindet einen Chiffrierzylinder, er war gleich der „wheel-cypher“

1891

der französische Major Etienne Bazeries erfand einen Chiffrierzylinder, sein BAZERIES-Zylinder war der „wheel cypher“ im Prinzip ähnlich

1922

wurde T.Jeffersons „wheel-cypher“ in den U.S.A. entdeckt, von der US-Marine weiterentwickelt und fand so bis in den 2.Weltkrieg Anwendung

1854

Der englische Physiker Charles Wheatstone erfand einen Chiffre, der mit einer 5*5 Matrix arbeitet. Sein Freund Lord Lyon Playfair Baron von St. Anrews machte diesen Chiffre in den höheren militärischen und diplomatischen Kreisen des viktorianischen Englands bekannt, der Chiffre bekam so den Namen „PLAYFAIR“-Code.

1860

Friedrich Kasiski und William F. Friedmann entwickeln statistische Methoden zur Kryptoanalyse.

1863

Der preußische Offizier Friedrich Kasiski a.D. (1805-1881) veröffentlicht in Berlin sein kryptologisches Werk mit dem Titel „Die Geheimschriften und die Dechiffrierkunst“, in dem er als erster ein Verfahren zur Lösung von polyalphabetischen Chiffren vorschlug. Mit diesem Verfahren konnte auch der bis dahin unlösbare Vigenère-Code geknackt werden.

1883

„La Cryptographie militaire“ von Auguste Kerkhoff von Nieuwendhoff erscheint.Es gilt als Meilenstein in der Kryptographie der Telegraphenzeit. Beinhaltet die „Prinzipien von Kerkhoff“ für die strategische Kryptologie

1917

Der Amerikaner Gilbert S. Vernam entdeckt und entwickelt das „ONE-TIME-PAD“

1921

Der Kalifornier Edward Hebern baut die erste Chiffriermaschine nach dem ROTOR-Prinzip.

1923

Vorstellung der vom dt. Ingenieur Arthur Scherbius entwickelten Rotormaschine „ENIGMA“ auf dem internationalen Postkongreß Gründung der „Chiffriermaschinen AG“, somit vermarktet A. Scherbius seine Enigma in alle Welt

1926

die deutsche Reichsmarine führt den Funkschlüssel C ein (Codierung der Nachrichten mit einer Enigma vom Typ C)

1941

Decodierung der japanischen Angriffsmeldung für den 2. Weltkrieg (viele Historiker meinen, daß die Kryptologie im 2. Weltkrieg ein Jahr Krieg erspart hat)

1950

Weltweit erfindet jedes größere Land eigene Chiffriermaschinen:

England: TYPEX

Japan: PURPLE

U.S.A.: SIGABA (M-134-C;ECM Mark 2)

1975

Diffie und Hellmann zeigen, daß PUBLIC-KEY-Verfahren theoretisch möglich sind, obwohl sie das Gegenteil beweisen wollten

1977

Das ab 1975 von IBM entwickelte DES (Data Encryption Standard) wird zum Standardverfahren auserkoren.

1978

Das nach seinen Entwicklern Ronald Rivest, Adi Shamir und Leonard Adleman benannte RSA-Verfahren wird veröffentlicht. Es ist das erste praktisch einsetzbare Public-Key-Verfahren und es gilt als innovativster Beitrag der kryptologischen Forschung unseres Jahrhunderts

1985

Goldwasser, Micali und Racoff stellen sog. ZERO-KNOWLEDGE-Verfahren vor

1990

Xueija Lai und James Massey entwickeln das IDEA-Verfahren, das z.B. in der Kryptologiesoftware PGP (Pretty Good Privacy)2840 von Phillip Zimmermann eingesetzt wird.


Allgemeine Theorie

Prinzipien des Auguste Kerckhoff

Auguste Kerckhoffs von Nieuwenhof geboren 1835 in den Niederlanden, studierte in Deutschland und lebte schließlich in Frankreich, wo er 1903 verstarb. Er schrieb unter anderem ein Buch zu Volapürük, einer künstlichen, Esperanto-ähnlichen Sprache.


Er galt als einer der bedeutensten Kryptographen der Telegraphenzeit und unterschied zwischen taktischen und strategischen Zielen der Geheimhaltung, also dem zeitweiligen Schutz und den zeitlosen Schutz der Nachricht und attackierte die bis dahin bei den Kryptologen gültige Formel


„Melius est abundare quam deficere“ - „Lieber zuviel als zu wenig“


Er forderte, daß die Sicherheit ganz oder zumindest zu einem wesentlichen Teil vom Schlüssel abhängen muß. Auguste Kerckhoffs beschreibt die Voraussetzungen für eine sichere Verschlüsselung folgendermaßen: "Ein Verfahren ist dann sicher, wenn man es nicht knacken kann, obwohl man den Code kennt." 1883 beschreibt Auguste Kerckhoffs in seinem Buch 'La Cryptographie Militaire', die folgenden sechs Regeln, gewonnen aus seinen Studien der historischen Kryptographie, die jeder befolgen sollte, wenn er sein Geheimnis bewahren will:


Diese Regeln ergänzend forderte Kerckhoffs, daß ein Chiffriersystem von Experten gut untersucht sein sollte.


Prinzipien Shannons

Der amerikanische Mathematiker Claude Shannon, geboren 1916 gilt als der Vater der Informationstheorie. Unter anderem beschäftigte er sich auch mit künstlicher Intelligenz, sowie mit künstlichen Schachautomaten.

In seinem Buch „Mathematical Theory of Communication“ revolutionierte er die Nachrichtentechnik genauso grundlegend, wie in seinem wissenschaftlichen Beitrag „Communication Theory of Secrecy Systems“, welchen er 1949 veröffentlichte und indem er seine kryptologischen Theoreme darstellte:





Das theoretisch perfekte Kryptosystem ist, wenn man die Aussagen von Kerckhoffs und Shannon zusammen nimmt, ein System, was:


Das Verfahren, das diese Annahmen erfüllt, gibt es und heißt One-Time-Pad. Leider sind nicht alle Prinzipien unter einen Hut zu bringen, wenn es um praktikabele Lösungen geht. Beim One-Time-Pad zum Beispiel ist der Schlüssel viel zu lang, oder die Erzeugung von Zufallsfolgen macht Probleme. Doch wenn man nochmal Kerckhoffs zu Rate zieht, dann gilt:


Wenn es praktisch sicher ist, bis die Information, die geheimgehalten werden sollte, durch die Zeit wertlos geworden ist, dann hat das Chiffriersystem seinen Zweck erfüllt.


Klassische Verfahren

Substitutionsverfahren

Die Grundidee dieser Gruppe von Verfahren ist es, die Buchstaben des Klartextes mit Hilfe einer Zuordnungstabelle durch andere Symbole zu ersetzen. Diese Symbole können Sonderzeichen, Buchstaben oder Zahlen sein. Man unterscheidet monoalphabetische Chiffren, bei denen der gesamte Text mit einer festen Zuordnungstabelle verschlüsselt wird und polyalphabetische Chiffren, die mehrere Zuordnungstabellen im Wechsel verwenden. Im folgenden werden verschiedene praktisch verwendete monoalphabetische Chiffren erläutert. Der Vigère-Code als Repräsentant für polyalphabetische Chiffren wird weiter unten dargestellt.



Beispiel:

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

L

D

T

A

I

N

G

U

X

H

O

S

Z

R

B

C

E

F

J

K

M

P

Q

V

W

Y



MEIN NAME IST HASE

ZIXR RLZI XJK ULJI



Werden als Geheimzeichen Zahlen verwendet, ergibt sich z.B. folgende Tabelle:

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26



M E I N N A M E I S T H A S E

13/5/9/14/ /14/1/13/5/ /9/19/20/ /8/1/19/5



Eines der bekanntesten klassischen Verschlüsselungsverfahren wurde nach Cäsar benannt. Dieser benutze es für den Briefwechsel mit seinen Statthaltern, Generälen und Konsuln.

Die Nachricht wird verschlüsselt indem man jeweils eine bestimmte Anzahl von Buchstaben im Alphabet weitergeht.

Angabe der Methode: A=B, A=C, A=D,...



Bildung der Schlüsselzeile:

z.B.: A=D

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

A

B

C



PROJEKT MACHT SPASS

SURMHNW PDFKW VSDVV,A=D



Die Substitutionsmethode mit A=N ist eine Sonderform des Cäsar-Codes. Sie zeichnet sich dadurch aus, daß die Zuordnung der Buchstaben symmetrisch ist, d.h. (A=N, N=A usw.). Dieses Verfahren ist auch als ROT13-Verfahren bekannt, weil die Buchstaben um 13 Stellen rotiert werden.

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

A

B

C

D

E

F

G

H

I

J

K

L

M



Ein sehr altes Verfahren ist das um 600 v.Chr. in Palästina angewandte Atbash-Verfahren, bei dem das Schlüssel-Alphabet in umgekehrter Reihenfolge dem Klartextalphabet zugeordnet wurde.

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

Z

Y

X

W

V

U

T

S

R

Q

P

O

N

M

L

K

J

I

H

G

F

E

D

C

B

A





Transpositionsverfahren

Beim Transpositionsverfahren werden die Zeichen des Klartextes nicht durch andere ersetzt, sondern lediglich in der Reihenfolge vertauscht.

Grundprinzip

Als Grundlage dient eine Matrix in die das zu chiffrierende Wort zeilenweise eingetragen wird. Die Anzahl der Spalten ist der geheime Schlüssel. Daraus und aus der Gesamtlänge des Klartextes ergibt sich die Anzahl der Zeilen in der Matrix. Das Chiffre wird durch spaltenweises Auslesen der Matrix gebildet.

Beispiel:

Matrix mit Schlüssel 6

I

C

H

B

I

N

D

E

R

D

O

K

T

O

R

E

I

S

E

N

B

A

R

T



spaltenweise ausgelesen: IDTECEONHRRBBDEAIOIRNKST

Das noch im Jahr 1917 vom deutschen Heer eingesetzten Drehraster basiert auf diesem Verfahren.



Einfache Spalten-Transposition

Alternativ dazu kann man die Matrix auch nach einer vorgegebenen Permutation spaltenweise auslesen.

Beispiel:

Schlüssel 4

Auslesepermutation 3421

1

2

3

4

E

S

W

A

R

S

C

H

O

N

D

U

N

K

E

L



permutiert ausgelesen: WCDE AHUL SSNK ERON



Doppelte Spalten-Transposition

Wird der durch einfache Spalten-Transposition gewonnene Chiffre erneut in die Matrix eingeschrieben und nochmals ausgelesen, erhöht man die Sicherheit des Chiffres.

Beispiel von oben weitergeführt:

Schlüssel 4

Auslesepermutation 3421

1

2

3

4

W

C

D

E

A

H

U

L

S

S

N

K

E

R

O

N



erneut permutiert ausgelesen: DUNO ELKN CHSR WASE



Gemischte Zeilen- und Spalten-Transpositionen

Bei dieser Abwandlung des Verfahrens wird nicht nur das Auslesen, sondern auch das Einschreiben in die Matrix permutiert.

Beispiel:

Schlüsel 4

Einschreibepermutation der Zeilen 2413

Auslesepermutation der Spalten 2143

1

2

3

4

4

5

6

7

8

3

13

14

15

16

2

1

2

3

4

1

9

10

11

12



Chiffre: 6 14 2 10 5 13 1 9 8 16 4 12 7 17 3 11



Block-Transposition

Der Klartext wird hierzu in gleichgroße Blöcke unterteilt, die jeweils mit dem gleichen Transpositionsverfahren chiffriert weren.

Beispiel:

Schlüssel 4

Permutation 3421

ESWA RSCH ONDU NKEL

WASE CHSR DUNO ELKN



Dechiffrierung

Mit der Kenntnis des Schlüssels, des verwendeten Algorithmus und der Länge des Geheimtextes kann die Matrix wiederhergestellt und rückwärts ausgelesen werden. Dabei erhält man den Klartext zurück.

Ohne Kenntnis des Schlüssels muß man auf Kryptoanalyse zurückgreifen. Dabei versucht man, aus Zeichenhaufen sinnvolle Kombinationen (Anagramme) zu bilden. Eine weitere Hilfe ist das Aufstellen von Häufigkeitsstatistiken (z.B. Bigramme, Trigramme), wenn der Klartext einer natürlichen Sprache entstammt.



Kombinatorische Komplexität

Darunter versteht man die Anzahl der möglichen Vertauschungen, um aus einem Klartext einen Chiffre zu erzeugen. Je höher dieser Wert ist, desto sicherer ist das Verfahren.

k

5

10


k!

120

3.628.800

Einfache Spalten-Transp.

(k!)²

14.400

1,32*1013

Gemischte Zeilen- oder Spalten-Transp.

(k²)!

1,55*1025

9,33*10157

Allgemeine Transp.



Dabei ist k die Anzahl der Spalten/Zeilen in einer quadratischen Matrix. Wie man leicht sieht ergeben sich bei einer Zeilen-/Spaltenzahl von k=5 120 Vertauschungsmöglichkeiten bei einer einfachen Spaltentransposition.

Um die Sicherheit noch weiter zu erhöhen kann man eine bitweise Transposition verwenden, die Spaltenanzahl erhöhen , an vorher vereinbarten Stellen sinnlose Zeicher (Blender) einfügen oder den Klartext vorher komprimieren.



Playfair-Chiffre


Der Name geht auf den britischen Lord Playfair zurück, welcher Gesundheitsreformen durchführte und Sprecher im House of Common war. Eigentlich wurde das Verfahren aber von Charles Wheatstone erfunden. Diese Herren waren miteinander durch ihr gemeinsames Hobby verbunden - Kryptologie. Beide knackten chiffrierte Anzeigen in der TIMES, und deshalb schlug Wheatstone ein neues Verfahren vor, was aber erst durch Playfair veröffentlicht wurde, aber nicht ohne den wahren Erfinder zu nennen. Die Playfair-Verschlüsselung wurde in diplomatischen Kreisen und vor allem beim Militär verwendet, zum Teil heute noch. In beiden Weltkriegen war dieser Algorithmus durch seine einfache Handhabung weit verbreitet.


Der Algorithmus beruht auf der Verschlüsselung von Buchstabengruppen, nicht von einzelnen Zeichen, dadurch wird die Häufigkeit verschleiert. Als Grundlage dient eine 5*5 Matrix.


G

R

U

E

N

S

P

A

B

C

D

F

H

I/J

K

L

M

O

Q

T

V

W

X

Y

Z


Das Schlüsselwort, in diesem Fall „Gruenspan“ wird eingetragen, und sich wiederholende Buchstaben werden weggelassen. Anschließend werden die restlichen Buchstaben des Alphabetes der Reihe nach eingetragen. I und J teilen sich ein Feld, was jedoch kaum Nachteile bringt [PLAYFAR].


Der Verschlüsselungsvorgang

Der Klartext wird in Zweiergruppen zerlegt. Bei doppelten Buchstaben muß ein vereinbartes Zwischenzeichen eingefügt werden z.B. X. Diese Zweiergruppen werden nun nach folgendem Schema chiffriert.

Liegen beide Buchstaben in einer Zeile der Matrix, werden jeweils die beiden Zeichen rechts davon als Chiffre notiert.

Liegen sie in ein und derselben Spalte werden jeweils die beiden Zeichen darunter notiert. Wenn die Buchstaben weder in der gleichen Zeile noch in der gleichen Spalte liegen notiert man die beiden Eckpunkte des gebildeten Rechtecks.


Beispiel:


die katze trat die treppe krumm => Zerlegung in Zweiergruppen


DI EK AT ZE TR AT DI ET RE PX PE KR UM MX => Buchstabenpaare in Matrix suchen


aus DI wird FK

aus EK wird NI (Ecken vom ersten Buchstaben an im Uhrzeigersinn)

usw.


es entsteht:


FK NI CO NY NM CO FK QN UN WA NF RO WO


Der Entschlüsselungsvorgang

  1. Text in Zweiergruppen einteilen

  2. Matrix mit richtigem (aktuellem) Schlüsselwort benutzen

  3. Zweiergruppen rückwärts verschlüsseln



Die Sicherheit

Im Playfair-Chiffre fallen häufig auftretende Buchstaben nicht mehr so auf, dafür treten die Bigramme mehr in den Vordergrund, deren Wahrscheinlichkeitsverteilung aber ausgeglichener ist. Der Ansatz für die Kryptoanalytiker ist, daß jedes Zeichen nur 5 versch. Bilder hat, seine 4 Nachbarn und das Zeichen unter ihm.

Häufige Buchstabengruppen stehen neben oder in der Zeile des E’s.

Der Vorteil dieses Verfahrens ist es, dass mit einer Teilentschlüsselung noch nicht der gesamte Klartext erschlossen werden kann.

Vigenère-Chiffre

Die Vigenère-Verschlüsselung ist die bekannteste unter allen polyalphabetischen Chiffren. Sie wurde im Jahre1586 von dem französischen Diplomaten Blaise de Vigenère (1523 bis 1596) der Öffentlichkeit zugänglich gemacht. Der Hauptgedanke dieser Methode ist, verschiedene monoalphabetische Chiffren im Wechsel zu benutzen. Zur Chiffrierung der Nachrichten nach dem Algorithmus von Vigenère braucht man unbedingt ein Schlüsselwort und das Vigenère-Quadrat. Ohne Schlüsselwort kann man nicht sagen, welche Geheimtextzeichen den Klartextzeichen entsprechen. Dabei kann das Schlüsselwort jede beliebige Buchstabenfolge sein.

Um diese Verschlüsselungsmethode zu demonstrieren nehmen wir ein Beispiel. Wir wählen ein beliebiges Schlüsselwort, z.B. „HALLO“ und schreiben dieses Wort zeichenweise über den Klartext, und zwar so lange, bis die Länge des Klartextes erreicht ist:
 

Schlüsselwort:      H A L L O H A L L O H A L
Klartext:           k r y p t o g r a p h i e
Geheimtext:         R R J A H V G C L D O I P
 

Das Schreiben des Geheimtextes ist wie folgt zu erklären: Der über einem bestimmten Klartextzeichen stehende Schlüsselwortbuchstabe und der direkt darunterliegende Klartextbuchstabe bestimmen anhand des Vigenère-Quadrates das Chiffre-Alphabet, mit dem der Klartextbuchstabe zu verschlüsseln ist.[BEUTLSP]

Also: den ersten Geheimtextbuchstaben „R“ bekommen wir, wenn wir im Vigenère-Quadrat in der Zeile „H“ und der Spalte „k“ nachschauen. Weiter suchen wir in der Zeile „A“ den Buchstabe in der Spalte „r“; dieser ist ebenfalls ein „R“. (Das ist nur ein Zufall, daß zwei gleiche Geheimtextbuchstaben hintereinander stehen.) In gleicher Weise führen wir die Verschlüsselung weiter durch.
 

Aufbau des Vigenère-Quadrates:

a b c d e f g h i j k l m n o p q r s t u v w x y z
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
B C D E F G H I J K L M N O P Q R S T U V W X Y Z A
C D E F G H I J K L M N O P Q R S T U V W X Y Z A B
D E F G H I J K L M N O P Q R S T U V W X Y Z A B C
E F G H I J K L M N O P Q R S T U V W X Y Z A B C D
F G H I J K L M N O P Q R S T U V W X Y Z A B C D E
G H I J K L M N O P Q R S T U V W X Y Z A B C D E F
H I J K L M N O P Q R S T U V W X Y Z A B C D E F G
I J K L M N O P Q R S T U V W X Y Z A B C D E F G H
J K L M N O P Q R S T U V W X Y Z A B C D E F G H I
K L M N O P Q R S T U V W X Y Z A B C D E F G H I J
L M N O P Q R S T U V W X Y Z A B C D E F G H I J K
M N O P Q R S T U V W X Y Z A B C D E F G H I J K L
N O P Q R S T U V W X Y Z A B C D E F G H I J K L M
O P Q R S T U V W X Y Z A B C D E F G H I J K L M N
P Q R S T U V W X Y Z A B C D E F G H I J K L M N O
Q R S T U V W X Y Z A B C D E F G H I J K L M N O P
R S T U V W X Y Z A B C D E F G H I J K L M N O P Q
S T U V W X Y Z A B C D E F G H I J K L M N O P Q R
T U V W X Y Z A B C D E F G H I J K L M N O P Q R S
U V W X Y Z A B C D E F G H I J K L M N O P Q R S T
V W X Y Z A B C D E F G H I J K L M N O P Q R S T U
W X Y Z A B C D E F G H I J K L M N O P Q R S T U V
X Y Z A B C D E F G H I J K L M N O P Q R S T U V W
Y Z A B C D E F G H I J K L M N O P Q R S T U V W X
Z A B C D E F C H I J K L M N O P Q R S T U V W X Y
 

Die Verschlüsselungsmethode von Vigenère wurde bereits in den frühen Jahren geknackt. Der erste Angriff wurde 1863 von dem preussischen Infanteriemajor Friedrich Wilhelm Kasiski (1805 bis 1881) veröffentlicht. Der zweite wurde im Jahr 1925 von Colonel William Frederick Friedman (1891 bis 1969) entwickelt. Die beiden Verfahren, der Kasiski-Test und der Friedman-Test, gelten als äußerst wichtig in der Kryptoanalyse.

Obiges Beispiel zeigt die Funktionionsweise des Vigenère-Chiffres recht anschaulich. Im Zeitalter der Computer ist es jedoch möglich, ja sogar notwendig die Vorgehensweise zu algorithmieren und mathematisch auszudrücken. Die mathematische Beschreibung des Vigenère-Verfahrens sieht nun folgendermaßen aus:

    Geheimtext = Klartext + Schlüssel

Man kann dies leicht nachvollziehen, wenn man den Buchstaben des Alphabets Zahlen zuordnet: A=0, B=1, C=2, ... , Z=25
Im obigen Beispiel sieht das so aus:
    K + H = ?  H=7; K=10 -> 10+7=17  ->  17=R
Die Umkehrung lautet Klartext = Kryptogramm - Schlüssel, also
    R - H = ?   -> 17-7=10 -> 10=K

Da diese Gleichung drei Variablen besitzt kann man noch zwei andere Rechenoperationen ausführen.

    Kryptogramm = Schlüssel - Klartext  ( Beaufort-Chiffre 1)
    Kryptogramm = Klartext - Schlüssel  ( Beaufort-Chiffre 2)

Diese Rechenoperationen sind analog zu obigem Beispiel auszuführen und stellen lediglich eine Abwandlung des Vigenère-Verfahrens dar. Im folgenden werden noch weitere Abwandlungen dieses Verfahrens dargestellt. [ALLGEMN]

Der Schlüssel von Gronsfeld

  a b c d e f g h i j k l m n o p q r s t u v w x y z
0 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
1 B C D E F G H I J K L M N O P Q R S T U V W X Y Z A
2 C D E F G H I J K L M N O P Q R S T U V W X Y Z A B
3 D E F G H I J K L M N O P Q R S T U V W X Y Z A B C
4 E F G H I J K L M N O P Q R S T U V W X Y Z A B C D
5 F G H I J K L M N O P Q R S T U V W X Y Z A B C D E
6 G H I J K L M N O P Q R S T U V W X Y Z A B C D E F
7 H I J K L M N O P Q R S T U V W X Y Z A B C D E F G
8 I J K L M N O P Q R S T U V W X Y Z A B C D E F G H
9 J K L M N O P Q R S T U V W X Y Z A B C D E F G H I

Dieses Verfahren benutzt nur 10 der 26 möglichen Schlüssel des Vignere-Verfahrens, also nur die Schlüsselalphabete A bis J, die in diesem Verfahren durch die Zahlen 0 bis 9 dargestellt werden. Damit kann man anstatt eines Schlüsselwortes eine Zahlenreihe verwenden. Dieses Verfahren ist aber wesentlich leichter zu knacken, da es für jeden Buchstaben nur 10 verschiedene Verschlüsselungsmöglichkeiten gibt. Ein Z im verschlüsselten Text kann somit z.B. nur den Buchstaben Q-Z entsprechen - niemals können die Buchstaben A-P durch ein Z verschlüsselt werden. Damit ist die Leistungsfähigkeit des Verfahrens sehr eingeschränkt.

Der Schlüssel des Trithemius

Bei diesem Verfahren verwendet man als Schlüsselwort das gesamte Alphabet, d.h. der Klartext wird der Reihe nach mit A B C ... X Y Z verschlüsselt. Damit ist zwar einem wichtigen Kriterium - der Schlüssellänge - Genüge getan, aber diesen Schlüssel geheimzuhalten bedeutet, das Verfahren geheimzuhalten. Wenn das Verfahren bekannt wird ist die Verschlüsselung praktisch nutzlos.

Angriffspunkte für die Kryptoanalyse - der Kasiski-Test

1863 stellte der preußische Infanteriemajor Friedrich Wilhelm Kasiski erstmals ein Verfahren zur systematischen Analyse und Dechiffrierung von mit Vignére verschlüsselten Botschaften dar. Das Verfahren stützt sich darauf, daß sich ein im Verhältnis zur Textlänge relativ kurzes Schlüsselwort ständig wiederholt. Dadurch kann es auftreten, daß zwei gleiche Wörter des Klartextes auch im verschlüsselten Text gleich sind. Dies ist immer dann der Fall, wenn der Abstand zwischen diesen Wörtern ein Vielfaches der Schlüsselwortlänge ist. Bei einem 5 Buchstaben langen Schlüsselwort würden also zwei gleiche Wörter im Abstand von 5, 10, 15, 20, ... Buchstaben gleich verschlüsselt werden. Kasiski ging nun so vor, daß er sich im verschlüsselten Text möglichst lange Buchstabenkombinationen suchte, die mehrfach auftraten und den Abstand dazwischen zählte. Diese ermittelten Abstände sind ein Vielfaches der Schlüsselwortlänge. Diese Vorgehensweise läßt sich recht einfach automatisieren, indem man den verschlüsselten Text gegen sich selbst verschiebt und die Übereinstimmung der Buchstaben zählt. Ist die Verschiebung gleich oder ein Vielfaches der Schlüsselwortlänge tritt eine markant hohe Übereinstimmung auf.
Beispiel mit Schlüssellänge 5:

AUSDENALTENSAGENKENNENWIRDENNAMEN   - Klartext
HALLOHALLOHALLOHALLOHALLOHALLOHAL   - Schlüssel

HUDOSUAWESUSLRSUKPYBLNHTFKEYYOTEY   - Verschlüsselte Nachricht
UDOSUAWESUSLRSUKPYBLNHTFKEYYOTEYH   1 Korrelationen bei Verschiebung 1
DOSUAWESUSLRSUKPYBLNHTFKEYYOTEYHU   1 Korrelationen bei Verschiebung 2
OSUAWESUSLRSUKPYBLNHTFKEYYOTEYHUD   1 Korrelationen bei Verschiebung 3
SUAWESUSLRSUKPYBLNHTFKEYYOTEYHUDO   2 Korrelationen bei Verschiebung 4
UAWESUSLRSUKPYBLNHTFKEYYOTEYHUDOS   6 Korrelationen bei Verschiebung 5
AWESUSLRSUKPYBLNHTFKEYYOTEYHUDOSU   0 Korrelationen bei Verschiebung 6
WESUSLRSUKPYBLNHTFKEYYOTEYHUDOSUA   3 Korrelationen bei Verschiebung 7
ESUSLRSUKPYBLNHTFKEYYOTEYHUDOSUAW   1 Korrelationen bei Verschiebung 8
SUSLRSUKPYBLNHTFKEYYOTEYHUDOSUAWE   3 Korrelationen bei Verschiebung 9
USLRSUKPYBLNHTFKEYYOTEYHUDOSUAWES   4 Korrelationen bei Verschiebung 10

Weiß man nun die Schlüssellänge kann man den Text sortieren nach Buchstaben, die mit dem selben Schlüsselbuchstaben verschlüsselt wurden. Bei der Schlüssellänge 5 nimmt man also den 1., 6., 11.,... in eine Gruppe, dann den 2., 7., 12., ... usw. Diese einzelnen Gruppen kann man nun statistisch analysieren. Man braucht dabei nur ein Klartext-Chiffre-Buchstabenpaar zu finden, da alle Buchstabe in einer Gruppe um den selben Wert verschoben sind. Man sucht also z.B. nach dem E, welches in den europäischen Sprachen der häufigste Buchstabe ist. Findet man nun z.B in einer Gruppe das H am häufigsten auf kann man davon ausgehen, daß diese Gruppe um 3 Stelle verschoben ist (Schlüssel=Kryptogramm-Klartext; H-E=D) Der Schlüsselbuchstabe dieser Gruppe ist also D. Dasselbe macht man mit allen Gruppe und erhält so das Schlüsselwort.

Autokey-/Fall Forward -Verfahren

Beim Autokey-Verfahren wird das Schlüsselwort nur einmal zum Verschlüsseln der ersten Buchstaben verwendet. Die folgenden Buchstaben werden mit den Klartextbuchstaben am Anfang beginnend verschlüsselt.

AUSDE|NALTE|NSAGE|NKENN|ENWIR|DENNA|MEN   - Klartext
HALLO|AUSDE|NALTE|NSAGE|NKENN|ENWIR|DEN   - Schlüssel
HUDOS|NUDWI|ASLZI|ACETR|RXAVE|HRJVR|PIA   - Verschlüsselte Nachricht


_______________________________________

Sgarro, Andrea: Geheimschriften. Augsburg: Weltbild, 1991. -ISBN 3-89350-162-2

Chiffrierzylinder


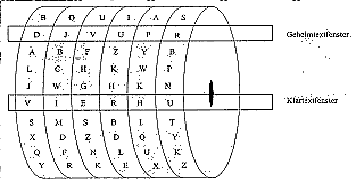
Der Chiffrierzylinder sieht wie folgt aus:


Grafik2 Chiffrierzylinder

Bild 2


Der Chiffrierzylinder besteht aus mehreren Scheiben, auf deren Ränder permutierte Alphabete eingraviert sind. Die Reihenfolge der Alphabete ist nicht wichtig und jede Scheibe hat eine andere Permutation. In der Abbildung hat der Chiffrierzylinder 6 Scheiben. Das heißt, jede Zeile enthält 6 Geheimtextzeichen. Der Schlüssel besteht in der Anordnung der Scheiben (hier Fakultät 6 Möglichkeiten).

Die bekanntesten Chiffriergeräte, deren Konstruktion auf den Chiffrierzylinder beruhen, sind die M-94 der US Army und das CSP-642 der Japaner. Die M-94 war von 1922 bis 1943 im Einsatz. Sie bestand aus 25 Aluminiumzylindern, bei denen nicht nur die Anordnung der Scheiben geheim war, sondern auch ihre Auswahl aus einer größeren Menge.


Rotormaschinen


Für Rotormaschinen wurden ab 1920 mehrere Patente eingereicht, wobei im folgenden Abschnitt nur der allgemeine mechanische Aufbau und die Funktionsweise der Rotormaschinen im Vordergrund stehen soll.

Rotormaschinen sind elektromechanische Verschlüsselungsgeräte. Sie bestehen, wie es der Name schon verrät, aus Rotoren. Rotoren sind dicke, elektronisch isolierte Scheiben, auf denen auf den gegenüberliegenden Flächen je 26 Schleifkontakte ringförmig angebracht sind und jeder Schleifkontakt einen Buchstaben des Alphabetes darstellt (Bild 3) .


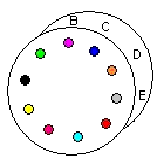
Bild3 Schleifkontakte vorn


Bild3 Schleifkontakte seitlich


Da jeder Schleifkontakt der linken Seite mit genau einem auf der rechten Seite verbunden ist, erhalten wir eine einfache Substitution.



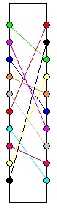
Nun werden auf der rechten Seite die Schleifkontakte mit je einem Lämpchen verbunden und auf der linken Seite wird an einem Kontakt eine Spannung angelegt. Das aufleuchtende Lämpchen ist abhängig von der inneren Verdrahtung des Rotors. Das Anlegen der Spannung kann man mit der Eingabe eines Zeichenes gleichsetzen, das Aufleuchten des entsprechenden Lämpchens ist vergleichbar mit der Ausgabe des chiffrierten Zeichens (durch Substitution).

Wenn wir nun nach jedem Zeichen den Rotor um eine Position weiter drehen, erhalten wir eine polyalphabetische Substitution (Bild 5/6/7) mit der Periode 26.


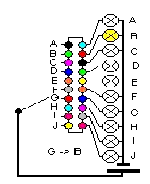
Bild7

Bild7


Nun wurden zur Erschwerung der Kryptoanalyse statt einer, mehrere Scheiben benutzt, hintereinander gestellt und über ihre Schleifkontakte verbunden. Die einzelnen Rotoren besitzen eine Rändelscheibe und ein Zahnrad, über die der Rotor während der Verschlüsselung mechanisch und manuell gedreht werden konnte. Auf Bild 8 sind zwei Enigmarotoren abgebildet, wobei beim oberen klar die Rändelscheibe und das Zahnrad, beim unteren die Schleifkontakte und das aufgedruckte Alphabet zu sehen sind.


Bild8 Enigmarotoren

Bild 8



Die Enigma

Die Enigma wurde im Jahr 1923 von Arthur Scherbius gebaut. Die ersten Modelle waren normale Rotormaschinen mit 4 Rotoren und dem oben beschriebenen Aufbau. Sie wurde seit dieser Zeit von der deutschen Wehrmacht verwendet und war bedeutend für den „Funkverkehr“. Im Jahre 1926 veränderte Willi Korn den Aufbau der Enigma.


Neuerungen in der Konstruktion von W. Korn


In seiner Konstruktion benutzt Korn nur noch 3 Rotoren, die nun allerdings einen beweglichen Ring hatten, auf dem die Zahlen 1-26 (das Alphabet) aufgedruckt waren. Über diesen Ring konnte nun die innere Verkabelung in bezug auf die äußere Numerierung geändert werden. Die Vorteile des Ringes waren eine Vergrößerung des Schlüsselraumes und ein zusätzlicher Schutz vor Spionage. Ohne den Ring konnte man von außen schon die Rotorpositionen des Rotorensystems erkennen.

Nun, da die relative Position von Verkabelung und Ring nicht zu sehen war, hatte man zwar die Ziffer, aber die eigentliche Rotorposition war unbekannt. Um das Verhältnis von Verkabelung und Ring zu ändern, mußte man den Rotor ausbauen.

Eine weitere Neuerung war ein vierter Rotor, der zur Anwendung kam. Dieser, auch als Reflektor bezeichnete Rotor, hatte nur auf einer Seite Schleifkontakte. Jeder Schleifkontakt war mit einem anderen des Reflektors fest verdrahtet.

Der Reflektor wurde fest an die äußerste rechte Seite gestellt und sollte die von links kommenden Signale auf einem anderen Weg zurück nach links „senden“.

Jedes Zeichen, das über die Tastatur eingegeben wurde, mußte zuerst von links nach rechts, dann auf einem anderen Weg von rechts nach links das Rotorensystem durchlaufen. Durch den Reflektor hatte die Enigma zwei neue Eigenschaften erhalten:


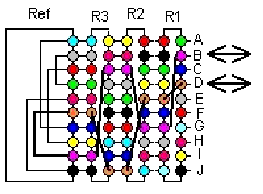
Bild9




Bild10

Bild 10


In schematischer Form kann man das Rotorensystem (Zerhacker) in Bild 9 sehen. Ein Enigma-Rotorensystem ist in Bild 10 zu sehen.


Eine weitere Neuerung, die vor und nach dem Rotorensystem zum Tragen kam,

war das Steckfeld (Bild 11).


Bild11


Über das Steckfeld konnten die Buchstaben vor und nach der Ver- und Entschlüsselung, durch das Rotorensystem, vertauscht werden. Dazu war es notwendig, eine Steckbrücke in die zu vertauschenden Buchstaben in das Steckfeld zu stecken. Die nicht gesteckten Buchstaben blieben unberührt.

Ein Beispiel zur Verdeutlichung der Arbeit des Steckfeldes:



Die letzte wichtige Neuerung war die Einführung einer Übertragsfunktion.

Sie arbeitete wie ein Kilometerzähler beim Auto. Nach der Eingabe eines Zeichens und der dazugehörigen Ausgabe des chiffrierten Buchstabens, wurde der äußerst links stehende Rotor stets um eine Position weiter gedreht. Wenn er nun eine Position erreichte, die durch eine veränderbare Kerbe am Rotor markiert ist und nun der Rotor noch einmal gedreht wurde, so führte die Mechanik der Enigma nicht nur diese Drehung des äußerst links stehenden Rotors aus, sondern auch eine Drehung um eine Position des rechts neben ihm stehenden Rotors. Die Kerbe konnte nur bei ausgebautem Rotor verändert werden. Solch eine Kerbe besaßen alle Rotoren.Bild12

Nur der letzte, dritte Rotor, gab keinen Übertrag weiter, denn der Reflektor war fest eingebaut und konnte somit nicht gedreht werden. Diese Einführung erhöhte die Periode von 26 auf 16900.


Bild 12


Diese von W. Korn erweiterte Version der Enigma wurde Enigma 1 genannt und wurde fortan von Heer, Luftwaffe und Marine benutzt. Auf Bild 12 sieht man eine Enigma und ihre Hauptbestandteile:



Die Enigma wurde später noch an einigen Stellen erweitert. So kamen im Laufe der Zeit immer weitere Rotoren zum Sortiment hinzu. Am Ende des 2.Weltkrieges sollen es etwa 10 Stück gewesen sein, aus denen man laut Codebuch die richtigen 3 aussuchen mußte und dann benutzte. 1942 wurde die Marine - Enigma um einen weiteren Rotor im Rotorensystem erweitert, so daß nun 4 Rotoren benutzt wurden, statt vorher 3. Im Allgemeinen gab es wegen der großen Anzahl dieser Chiffriermaschinen und der drei unabhängigen Waffengattungen auch eine große Menge unterschiedlicher Ausführungen in der Bauart und der Benutzung. Deshalb wurde oben nur der grundsätzliche Aufbau und die Funktionsweise der Rotormaschine - Enigma beschrieben.


Zum Gebrauch der Enigma


Bevor die Enigma zum Chiffrieren und Dechiffrieren benutzt werden konnte, mußten allgemeine und spezielle Einstellungen vorgenommen werden. Die allgemeinen Einstellungen betrafen die Punkte:


  1. welche Rotoren benutzt wurden und in welcher Reihenfolge (Auswahl/Anordnung)

  2. die für jeden Rotor verschiedenen Einstellungen für Übertrag und Ringposition auf dem Rotor

  3. welche Kombinationen auf dem Steckfeld gesteckt wurden (die Anzahl der Steckbrücken war zwischen 4 und 7)


Diese Einstellungen wurden durch Codebücher festgelegt. Die Codebücher waren immer auf einen Monat und jede Einstellung war auf 24 Stunden begrenzt. Nach dem diese 3 Punkte abgearbeitet waren, mußte man die Anfangspositionen der Rotoren einstellen. Diese Anfangspositionen waren nicht festgelegt. Somit mußte sich der Chiffreur die Positionen ausdenken. Das Problem war nun, daß zum dechiffrieren diese Positionen benötigt wurden. Somit mußte nicht nur der Text, sondern auch die Anfangspositionen mit gesendet werden. Dieses wurde so wie vieles unterschiedlich gehandhabt. Hier nur ein Beispiel zur Lösung des Problems.


Die Anfangspositionen werden am Anfang des Textes als Klartext übertragen.

Ein Beispiel (vereinfacht):



Sicherheit der Enigma


Zum Entschlüsseln eines, mit der Enigma, chiffrierten Textes, braucht man die Auswahl und Anordnung der Rotoren, die Rotorenausgangsstellung und die Beschreibung des Steckfeldes. Diese drei Punkte mußten unbedingt geheim gehalten werden. Die Enigma wurde von W. Korn und anderen Stellen als absolut sicher eingestuft. Diese Annahme wurde bis zum Ende des Krieges beibehalten und stützt sich auf den großen Schlüsselraum und die lange Periode.



Der Schlüsselraum, etwa 2*10^20, ergibt sich aus der Anzahl der zur Auswahl stehenden Rotoren (ca.10), der möglichen Ausgangsstellung der Rotoren, der Anzahl der verschiedenen Anordnungen der Rotoren im Rotorensystem , der Initialpermutation und der verschiedenen Steckfeldanordnungen. Die Periode der Enigma mit 3 Rotoren im Rotorensystem beträgt ca. 16900.

Aber die Enigma wurde trotz ihres großen Schlüsselraumes und der langen Periode, durch Angriffe von Polen und später England, gebrochen. Dieses folgt aus verschiedenen Schwachstellen im Umgang mit der Enigma und ihrem Aufbau selbst. Dieses wollen wir nun noch etwas tiefer betrachten.


Schwachstellen im Aufbau


Eine der Hauptschwachstelle der Enigma war, daß sie auf ein käufliches Chiffriergerät aufbaute. Weiterhin wurde sie in solchen Massen benutzt, daß es unmöglich war, den inneren Aufbau geheimzuhalten. Aber gerade dieser innere Aufbau, machte die Enigma erst so stark. Somit dürfte zum Beispiel das wichtige Geheimnis um die Innereverkabelung der Rotoren immer nur für absolut neu entwickelte Rotoren bestanden haben, dieses aber auch nur für einen kurzen Zeitraum. Außer dieser kaum zu verhindernden Schwachstelle, gab es verschiedene in der Enigma selbst. Hier zwei wichtige Beispiele:


  1. die Anschlüsse von Tastatur bzw. Lampenfeld zum ersten Rotor waren in alphabetischer Reihenfolge ringförmig angeordnet, eine Veränderung (Permutation) dieser Anschlüsse, hätte die Kryptoanalyse der Gegner stark erschwert und vielleicht sogar ohne eine genaue Beschreibung einer Maschine solchen Typs unmöglich gemacht

  2. die Erweiterung der Marine - Enigma um einen Rotor war nur halbherzig, denn dieser Rotor konnte nicht wie die anderen ausgetauscht werden, sondern wurde an seiner Stelle fest eingebaut. Daraus resultierte, daß der Schlüsselraum nur um den Faktor 26 statt 234 größer wurde


Schwachstellen in der Benutzung


Die allgemeinen Einstellungen wurden über Codebücher festgelegt und

waren somit für 24 Stunden bei allen Enigmamaschinen gleich. Dieses vereinfachte die Kryptoanalyse, denn wenn einmal die Tageseinstellungen bekannt waren, zum Beispiel über gefundene Codebücher oder über Kryptoanalyse, mußten bei allen Kryptotexten nur noch die Anfangsrotorpositionen herausgefunden werden. Es sollen auch Codebücher später mehrmals benutzt worden sein. Ein anderes Problem war die Übertragung

der Anfangsposition der Rotoren. Denn wie im oben beschriebenen Beispiel (Gebrauch der Enigma) die Positionen als Klarschrift voranzustellen, ist eigentlich zu einfach. Aber auch spätere System waren nur unmerklich besser. Die typisch deutschen Armeenachrichten, die sehr kurz und monoton waren, erhöhten ebenfalls nicht die Sicherheit. Aus ihnen konnten gute Kyptoanalytiker Schlüsse auf den Klartext ziehen und hatten somit einen Angriffspunkt. Hier soll nun auch kurz die Turingbomb erwähnt werden, die von Alan Turing, einem englischen Mathematiker, konstruiert wurde. Die Turingbomb ist ein Klartextangriff. Man benutzt Klartexte und ihre Chiffrierung, um auf die Rotorstellungen der Enigma zu schließen.


Ich denke, daß man die halbherzigen Änderungen darauf zurückführen kann, daß, wie oben schon mal angesprochen, bei den zuständigen Stellen in Deutschland niemand daran glaubte, daß die Enigma selbst gebrochen wurde und somit die Änderungen gegen "innere" Spionage anzusehen sind. Somit ist die Dechiffrierung der Enigma durch Polen und England in bezug auf Deutschland eher auf Ignoranz und Unwissen von Personen, als auf die technischen Mängel der Enigma, zurückzuführen.


Die Geschichte der Enigma nach 1945


Die Enigma wurde noch nach 1945 von Deutschland und der Schweiz nach Afrika, den Nahen Osten und Südamerika verkauft. Sie wurde dort für die militärische und diplomatische Kommunikation eingesetzt.

Ebenfalls sollen die USA die Enigma an Länder der 3.Welt verkauft haben, um Geheimnachrichten abhören zu können.

Beim heutigen Stand der Technik sollte die Enigma kaum noch den Angriffen gewachsen sein.


Benutzte Literatur und WWW - Seiten waren [GIESSMN],[ENIGMA1],[ENIMA2],[ENIGMA3][ENIGMA4]

Das Bildmaterial stammt von [ENIGMA5]


Moderne Verfahren

Der DES Algorithmus


Der DES Algorithmus ist ein Produktalgorithmus, speziell ein Feistel-Netzwerk. Er

- Verwendet einen 56 Bit langen Schlüssel, um

- blockweise 64 Bit Klartext in 64 Bit Geheimtext zu überführen bzw. umgekehrt. Das

geschieht

- in 16 schlüsselabhängigen Runden. Vor der ersten und nach der letzten Runde werden

- jeweils eine feste, bitweise Transposition durchgeführt. Dabei ist die abschließende

Permutation die Umkehrung der ersten.


Aufbau der runden- und schlüsselabhängigen Funktion f des DES

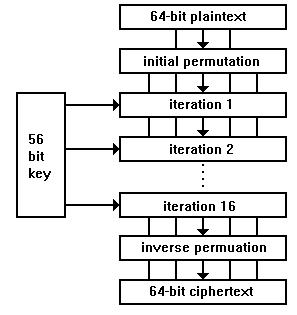
Bild DES-Runden

- Es werden 48 Bit, in Abhängigkeit der Runde des veränderten 56 Bit Schlüssels, ausgewählt.

- Die Rechte Blockhälfte wird von 32 auf 48 Bit erweitert.

- Beide 48 Bit-Folgen werden durch XOR verknüpft.

- Das Ergebnis wird mittels acht S-Boxen in eine 32 Bit-Folge transformiert

- Jetzt wird die 32 Bit-Folge durch eine P-Box permutiert.


Der entstandene 32 Bit Block braucht nun nur noch per XOR mit der linken Blockhälfte verknüpft zu werden,

und es ergibt sich die rechte Blockhälfte der neuen Runde. Die Dechiffrierung läuft, ganz ähnlich der Chiffrie-

rung, nur mit umgekehrter Reihenfolge der Rundenschlüssel ab.


Eingangs und Ausgangspermutation


Die Permutationen vor der ersten und nach der letzten Runde dienen keiner Sicherheit. Vermutlich liegt ihre

Verwendung in der Hardware begründet, denn Mitte der 70er Jahre war es noch nicht so einfach, 64 Bit Daten

in ein Register zu laden: Es gab noch nicht einmal 16 Bit Mikroprozessoren.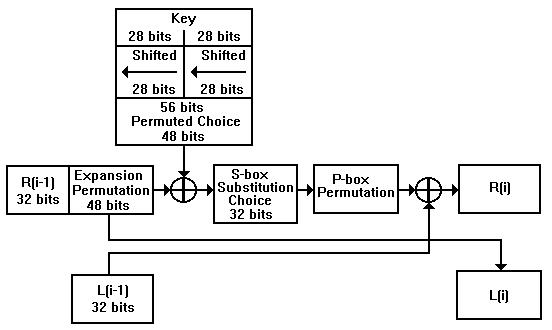Bild: DES-Permutation


RSA



RSA ist ein von Ron Rivest, Adi Shamir, Leonard Adleman entwickeltes asymmetrisches Public-Key-Verfahren. Es überstand eine jahrelange Kryptoanalyse und wird heute als Standardverfahren von fast allen gängigen Verschlüsselungssystemen eingesetzt.

Wie das Verfahren funktioniert, soll am folgenden Beispiel gezeigt werden:


Primzahlen: p, q p = 47 q = 71

Öffentlicher Schlüssel:

n = pq n = 47 * 71 = 3337

e - CS zufällig gewählt e = 79

! prim zu (p-1)(q-1) 46 * 70 = 3220

Privater Schlüssel:

d = DCS

d = e¹ mod ((p-1)(q-1)) d = 79¹ mod 3220 = 1019

d wird mit dem erweiterten Euklidischen Algorithmus (siehe unten) berechnet,

p und q werden nicht mehr benötigt, dürfen aber niemals bekanntgegeben werden

Verschlüsselung:

M = Nachricht M = 6882326879666683

Blöcke Þ m= 668; m= 232; m= 687

m= 966; m= 668; m= 003

ci = mie mod n c= 688 mod 3337 = 1570

C = c+ c+...+c C = 1570 2756 2096 2276 2423 158

Entschlüsselung:

mi = cid mod n m= 1570¹¹ mod 3337 = 688


Erweiterter euklidischer Algorithmus


Ziel: Bestimmung von d

1. Schritt: Bestimmung des ggT [e, (p-1)(q-1)]

ges.: d geg.: e = 79;

(p-1)(q-1) = 3220

Lsg.: 1 = ed mod (p-1)(q-1) 1 = 79 d mod 3220

3220 = 79 * 40 + 60

79 = 60 * 1 + 19

60 = 19 * 3 + 3

19 = 3 * 6 + 1 ggT = 1

3 = 3 * 1 + 0

2. Schritt: Gleichungskette von unten auflösen

1 = 19 – 3 * 6 die 3 aus 3. Zeile einsetzen 3 = 60 – 19 * 3

1 = 19 - [ ( 60 – 19 * 3 ) * 6 ]

1 = 19 * 19 – 60 * 6

1 = 19 ( 79 – 60 ) – 60 * 6

1 = 19 * 79 – 60 * 25

1 = 19 * 79 – ( 3220 – 79 * 40 ) * 25

1 = 19 * 79 – 3220 * 25 + 79 * 40 * 25 ( 79 zusammenfassen )

1 = 79 ( 19 – 3220 * 25 / 79 + 40 * 25 ) 79 ( 19 – 3220 * 25 / 79 + 1000 )

1 = 79 * 1019 – 3220 * 25

79 * 1019 mod 3220 = 1

d = 1019



Sicherheit von RSA

Die Sicherheit von RSA beruht auf dem Problem der Faktorisierung großer Zahlen. Liegen

p und q in der Größenordnung von 100 - 200 Stellen, so hat n 200 – 400 Stellen (Wir erinnern uns: n=p*q)

Die nächstliegende Angriffsmethode ist also die Faktorisierung von n, da mit dem öffentlichen

Schlüssel n und e bekannt sind.


Um also den privaten Schlüssel d zu berechnen muß man n faktorisieren. Zum heutigen Zeitpunkt nimmt man an, das Zahlen bis 129 Stellen in endlicher Zeit zu faktorisieren sind, so daß man mit der Wahl von n deutlich größer als 129 Stellen auf der sicheren Seite ist.


Ein weiterer möglicher Angriff wäre die Brute Force - Methode. Dabei wird jedes mögliche d probiert, bis man den richtigen Wert gefunden hat. Dies ist bei RSA allerdings noch ineffizienter als eine Faktorisierung von n, da d = e¹ mod ((p-1)(q-1)) ist.


RSA wird als praktisch sicher bezeichnet. Was bedeutet das?

Nun, wir haben gesehen, das die Anzahl der möglichen Schlüssel so groß ist, dass systematisches Durchprobieren ausgeschlossen ist. Damit wäre ein minimales Sicherheitskriterium erfüllt.RSA wurde durch seine Veröffentlichung gut untersucht, aber trotzdem als solcher nicht geknackt. Sein Schwachpunkt liegt einzig und allein in der Faktorisierung großer Zahlen. Er ist damit praktisch sicher, obgleich er theoretisch angreifbar ist.Sobald eine Möglichkeit gefunden worden ist, mehrere hundert Bit lange Zahlen zu faktorisieren, ist der RSA- Algorithmus praktisch wertlos.

Integrität und Authentizität von Nachrichten

Alle bisherigen Verfahren dienten dazu, zu übermittelnde Nachrichten gegen unberechtigtes Lesen abzusichern. In der Kryptologie heißt dieses Mitlesen passiver Angriff, da der Inhalt der Nachricht, deren Integrität, erhalten bleibt. Was passiert nun wenn der Kryptanalytiker, das ist die vornehme Variante, doch die Nachricht ändert, dann ist aus dem passiven Angriff ein aktiver geworden. Dies wirft natürlich gleich die zweite Frage auf - Wie sicher ist der Übertragungsweg überhaupt? Wenn man davon ausgeht, dass der Übertragungsweg keine Sicherheit bietet, so muß man sich Möglichkeiten schaffen, um die Echtheit von Nachrichten zu prüfen. Diese sollten ein Verfälschen der Nachricht sicherstellen. Daran schließt sich das Problem der Identität des Senders an, d. h. der Empfänger braucht Mittel um sich davon zu überzeugen, das dein Kommunikationspartner der ist, mit dem er wirklich kommunizieren will. Man spricht von Nachrichtenauthentikation.


Integrität von Nachrichten

Grundanliegen ist es, festzustellen ob die übermittelte Nachricht verfälscht oder verändert wurde.


Zwei Beispiele zur Sicherung der Integrität


Der kryptographische Fingerabdruck:


Message-Authentication-Code MAC



Cipher - Block - Chaining - Mode


Klartext wird in Blöcke gleicher Länge eingeteilt (typisch sind 64 Bit) m1, m2, ..., mn


MAC mittels Cipher - Block -Chaining -Mode


Benutzerauthentikation


Eine Grundaufgabe der Sicherheitstechnik ist es, die Identität von Personen sicherzustellen, das heißt sie zu authentifizieren.[BEUTLSP]


Personen können durch Wissen oder Besitz identifiziert werden.


Passwörter


Passwörter ohne Verschlüsselung



-sinnlos


Passwörter mit Verschlüsselung




Einwegfunktionen sind nicht oder nur sehr schwer umkehrbare Funktionen.

Challenge and Response Verfahren



Beispiel zwischen Chipkarte und Rechner


beider verfügen über geheimen Schlüssel k


Zero-Knowledge-Protokolle


Grundgedanke dieser Protokolle ist, jemanden davon zu überzeugen, dass man im Besitz eines Geheimnisses (Schlüssels) ist, ohne davon das Geringste zu verraten.


Historisches Beispiel: Das Geheimnis des Tartaglia (Lösung einer kubischen Gleichung)[BEUTLSP]


Das Fiat -Shamir -Protokoll



Funktionsmodell


Schlüsselzentrale



Benutzer Rechner




y




Der Verifizierer wird irgendwann davon überzeugt sein, dass der Benutzer das Geheimnis s besitzt.

Die Wahrscheinlichkeit für die Vorhersage des Bits b ist bei t-maliger Ausführung 1/2t. Nach 20 Durchläufen ist die Wahrscheinlichkeit kleiner als 1 zu einer Million.


Wichtig!! Auch nach dem Authentikationsprozess bleibt das Geheimnis s absolut geheim.


Anwendungen


Am Anfang hatten wir die These aufgestellt, jeder in unserer heutigen Gesellschaft hat mit Kryptologie in irgendeiner Art und Weise zu tun. Bisher haben wir die zeitliche Entwicklung der Kryptologie dargestellt und einen groben Überblick über die wichtigsten Verfahren gegeben.Vielleicht wurde an der einen oder anderen Stelle bewußt, warum die Anwendung kryptologischer Verfahren so bedeutungsvoll in dieser Zeit ist. Wir haben mehrere Umbrüche in der Entwicklung unserer Gesellschaft hinteruns. Angefangen mit der auf Landwirtschaft basierenden Zivilisation, über Handwerk bis hin zur Industriellen Revolution bewegen wir uns heute im Zeitalter der Information. Das Wissen Macht ist, wird dann deutlich, wenn Firmen Neuentwicklungen vor der Konkurrenz schützen wollen, wenn bestimmte Datenbanken nur gegen Entgelt durchforstbar sind, wenn Politiker peinlich-beschämende Vorgänge nicht veröffentlich wollen. Aber auch deine Privatsphäre und Sicherheit können gefährdet sein! Umfangreiche Banken-, Kreditkarten- und medizinische Datenbanken, eMail-Überwachung und Computerschnüffelprogramme sind nur einige wenige Faktoren, die jeden gesetzestreuen Bürger treffen. Kurz gesagt, unsere in Privatsachen schnüffelnde Gesellschaft dient den Kriminellen und serviert Deine Daten auf einem Silbertablett.


Im allgemeinen gilt, das klassische Sicherheitsaspekte der Integrität, Vertraulichkeit, Verfügbarkeit, Verbindlichkeit und Authentizität zunehmend allgemein gewünschte Merkmale von Kommunikationsprozessen sind. Sichere Kommunikation ist Vorraussetzung für wirtschaftliche und behördliche Netzteilnahme.


An dieser Stelle soll ein Überblick über die Anwendung kryptologischer Verfahren in der Praxis gegeben werden.


Einsatz von GnuPG und PGP


In Anlehnung an die nichttechnische PGP-FAQ40[PGPFAQ1], sowie an die Presseerklärung des BMWi [GNUPG1]40 soll hier ein Überblick über PGP und GnuPG gegeben werden.

Was ist PGP?

PGP (ausgeschrieben "Pretty Good Privacy" (ziemlich gute Privatsphäre)) ist ein Computerprogramm, das Daten verschlüsselt und entschlüsselt.

Philip Zimmermann schrieb das erste Programm. Phil -ein Held für viele Unterstützer des Datenschutzes- arbeitet als Sicherheitsexperte in Boulder, Colorado. Andere Programmierer aus der ganzen Welt haben an den nachfolgenden PGP Versionen und Benutzungsoberflächen mitgeholfen.

PGP benutzt das RSA23 Public-Key Verschlüsselungssystem. RSA wurde 1977 von seinen Erfindern vorgestellt: Ronald Rivest vom MIT, Adi Shamir vom Weizmann Institute in Israel und Leonard Adelman vom USC. Nach den Anfangsbuchstaben der Nachnamen dieser Leute wird es "RSA" genannt. PGP verwendet außerdem ein Verschlüsselungssystem namens IDEA welches 1990 von Xuejia Lai und James Massey entwickelt wurde.

Was ist GnuPG?

GnuPG ist eine von Werner Koch aus Düsseldorf entwickelte Verschlüsselungs-Software. GnuPG wird von Sicherheitsexperten in aller Welt als eines der derzeit besten Verschlüsselungssysteme anerkannt.

Das Besondere an GnuPG:

Wer benutzt PGP bzw. GnuPG Verschlüsselung (oder andere RSA-basierte Systeme)?

Leute, die Wert auf ihre Privatsphäre legen; Politiker, die Wahlkampagnen durchstehen; Steuerzahler, die ihre Steuererklärung abspeichern; Ärtze, die Patientendaten schützen; Unternehmer, die Firmengeheimnisse wahren müssen; Journalisten, die ihre Informanten schützen, und Menschen, die Kontakte suchen, sind nur einige wenige der gesetzestreuen Bürger, die PGP benutzen, um ihre Dateien und eMail geheim zu halten.

Geschäftleute benutzen ebenfalls PGP. Stell Dir vor, Du bist ein Geschäftsführer und mußt per eMail einen Angestellten nach seinem Vorankommen befragen. Du könntest gesetzlich verpflichtet sein, diese eMails geheimzuhalten. Stell Dir vor, Du bist eine Verkäuferin und Du mußt mit Deiner Zentrale über ein öffentliches Computernetzwerk hinweg, Deine Kundenliste pflegen. Deine Firma und der Gesetzgeber kann fordern, daß diese Liste geheim bleibt. Dies sind nur einige wenige Gründe weswegen im Geschäftsleben Verschlüsselung zum Schutz der Kunden, der Angestellten und der Firmen selbst eingesetzt wird.

PGP hilft auch bei sicheren Finanzübertragungen. Bspw. die Electronic Frontier Foundations (EFF) benutzt PGP zur Verschlüsselung von Mitgliedernummern, so daß die Mitglieder per eMail ihre Beiträge bezahlen können.

Thomas G. Donlan, ein Redakteur bei Barron's (einer Finanzpublikation, die zum The Wall Street Journal gehört), schrieb ein ganzseitiges Editorial am 25.April 1994. Barron's übertitelte es mit "Privacy and Security: Computer Technology Opens Secrets, And Closes Them." (Datenschutz und Datensicherheit: Computertechnik öffnet Geheimnisse und verschließt sie)

Mr. Donlan schrieb (auszugsweise):

"RSA Data Security, the company founded by the three inventors, has hundreds of satisfied customers, including Microsoft, Apple, Novell, Sun, AT&T and Lotus. Versions of RSA are available for almost any personal computer or workstation, many of them built into the operating systems. Lotus Notes, the network communications system, automatically encrypts all it messages using RSA. Other companies have similar products designed around the same basic concept, and some versions are available for free on computer bulletin boards."
RSA Data Security, gegründet von den drei Erfindern, hat Hunderte von zufriedenen Kunden, zu denen auch Microsoft, Apple, Novell, Sun, AT&T und Lotus gehören. Implementationen von RSA stehen in fast jedem Personalcomputer oder Workstation zur Verfügung, oft ins Betriebssystem eingebaut. Lotus Notes, das Netzkommunikationssystem, verschlüsselt automatisch alle Nachrichten mit RSA. Andere Firmen haben vergleichbare Produkte, entwickelt nach dem gleichen Prinzip, und einige Versionen sind in Mailboxen frei verfügbar.

Donlan fährt fort:

"Without security, the Internet is little more than the world's biggest bulletin board. With security, it could become the information supermarket of the world. RSA lets people and banks feels secure putting their credit-card numbers on the public network. Although it still seems that computers created an age of snoopery, the age of privacy is at hand."
Ohne Sicherheit ist das Internet nicht viel mehr als die weltgrößte Mailbox. Mit Sicherheit kann es der Informationssupermarkt der Zukunft werden. RSA gestattet es Menschen und Banken, sich bei der Angabe der Kreditkartennummer im öffentlichen Netz sicher zu fühlen. Obwohl es noch den Anschein hat, daß Computer ein Zeitalter der Schnüffelei begannen, liegt das Zeitalter der Privatsphären vor uns.

Sind nicht Computer und eMail schon sicher?

Deine Computerdateien (ohne Verschlüsselung) können von jedem gelesen werden, der Zugriff auf Deinen Rechner hat. EMail ist notorisch unsicher. Die typische eMail wandert über viele Systeme. Die Personen, die diese Systeme betreiben, können Deine Nachrichten lesen, kopieren und speichern. Viele Mitbewerber und Voyeure sind hochmotiviert eMail abzufangen. Eine geschäftliche, offizielle oder persönliche Nachricht mit dem Computer zu versenden, ist weniger geschützt als das gleiche auf einer Postkarte zu verschicken. PGP ist ein sicherer "Briefumschlag", der Mitbewerber und Kriminelle abhält, Dir zu schaden.

Ich habe nichts zu verbergen. Wozu brauche ich Datenschutz?

Zeig mir einen Menschen, der keine Geheimnisse vor seiner Familie, seinen Nachbarn oder seinen Kollegen hat und ich zeige Dir jemanden, der entwerder ein ungewöhnlicher Exhibitionist oder ein unglaublicher Dummkopf ist.

Zeige mir eine Firma, die keine Firmengeheimnisse hat und ich zeige Dir ein Geschäft, das nicht läuft.

In einem Brief schrieb mir ein Student folgendes:

"I had a part-time job at a dry cleaner. One day I returned a diamond ring that I'd found in a man's coat pocket to his wife. Unfortunately, it was NOT her ring! It belonged to her husband's girlfriend. His wife was furious and divorced her husband over this incident. My boss told me: 'Return jewelry ONLY to the person whose clothes you found it in, and NEVER return underwear that you find in pockets!' Until that moment, I thought my boss was a finicky woman. But she taught me the need for PGP."
Ich hatte einem einen Teilzeitjob als Reinigungskraft. Eines Tages brachte ich einen Diamantring, den ich in einer Manteltasche eines Mannes gefunden hatte, seiner Frau zurück. Unglücklicherweise war es NICHT ihr Ring! Er gehörte der Freundin ihres Mannes. Seine Frau wurde fuchsteufelswild und ließ sich wegen dieses Vorkommnisses scheiden. Mein Chef sagte mir: 'Gib Juwelen NUR der Person zurück, in deren Sachen Du es fandest. Und gib NIEMALS Unterwäsche zurück, die Du in einer Tasche fandest.' Bis zu diesem Moment dachte ich, mein Chef wäre eine engstirnige Frau. Aber sie lehrte mich die Notwendigkeit von PGP.

Geheimhaltung, Diskretion, Vertraulichkeit und Besonnenheit sind die Markenzeichen dieser Zivilisation.

Ich habe gehört, die Polizei sage, daß Verschlüsselung verboten werden soll, weil Kriminelle sie zur Tarnung benutzen. Ist das wahr?

Das nächste Mal, wenn Du jemanden das erzählen hörst, frag ihn, ob er Thomas Jefferson verbieten möchte, den "Vater der amerikanischen Kryptographie", der die amerikanische Unabhängigkeitserklärung schrieb.

Viele Regierungen, Firmen und Gesetzeshüter benutzen Verschlüsselung um ihre Operationen zu verstecken. Ja, einige Kirminelle benutzen auch Verschlüsselung. Kriminelle benutzen aber häufiger Autos, Handschuhe und Masken, um zu entkommen.

PGP ist "Verschlüsselung für die Massen". Es gestattet dem gesetzestreuen Durchschnittbürger einige der Schutzmaßnahmen, die die Regierungen und Firmen für sich beanspruchen.

Wie arbeiten PGP und GnuPG?

PGP und GnuPG sind "öffentliche Schlüsselsysteme" (public key cryptography). Wenn Du PGP bzw. GnuPG das erste Mal startest, generiert es zwei "Schlüssel", die nur zu Dir gehören. Stell Dir diese Schlüssel wie ein Gegenstück zu den Schlüssel Deiner Tasche vor. Ein PGP-Schlüssel ist der geheime Schlüssel und bleibt auf Deinem Rechner. Der andere Schlüssel ist öffentlich. Du gibst diesen öffentlichen Schlüssel Deinen Gesprächspartnern. Hier ist ein Beispiel eines öffentlichen Schlüssels:

-----BEGIN PGP PUBLIC KEY BLOCK-----
Version: 2.7

mQA9Ai2wD2YAAAEBgJ18cV7rMAFv7P3eBd/cZayI8EEO6XGYkhEO9SLJOw+DFyHg
Px5o+IiR2A6Fh+HguQAFEbQZZGVtbyA8ZGVtb0B3ZWxsLnNmLmNhLnVzPokARQIF
EC2wD4yR2A6Fh+HguQEB3xcBfRTi3D/2qdU3TosScYMAHfgfUwCelbb6wikSxoF5
ees9DL9QMzPZXCioh42dEUXP0g==
=sw5W
-----END PGP PUBLIC KEY BLOCK-----

Stell Dir vor, der öffentliche Schlüssel gehört zu Dir und Du mailst ihn mir. Ich kann Deinen öffentlichen Schlüssel in meiner PGP Software speichern und benutze Deinen öffentlichn Schlüssel, eine Nachricht zu verschlüsseln, die nur Du lesen kannst. Einer der Vorteile von PGP ist, daß Du mir diesen Schlüssel geben kannst, wie Deine Telefonnummer. Wenn ich Deine Telefonnummer habe, kann ich Dich anrufen; aber ich kann Dein Telefon nicht abheben. Ähnlich ist es mit dem öffentlichen Schlüssel: Ich kann Dir eine Nachricht verschlüsseln; Ich kann sie aber nicht lesen.

Dieses Konzept des public-key Schlüssels kann anfangs etwas seltsam klingen. Trotzdem wird es völlig klar, sobald Du etwas mit PGP rumspielst.

Wie sicher ist PGP bzw. GnuPG? Schützt es mich wirklich?

Vielleicht kann die Regierung oder Deine Schwiegermutter PGP Nachrichten "knacken", indem sie Supercomputer oder Genialität einsetzt. Davon habe ich keine Ahnung. Drei Dinge sind jedoch sicher:

  1. Hervorragende Kryptoanalytiker und Computerexperten haben vergeblich versucht, PGP zu knacken.

  2. Wer auch immer nachweist, daß er PGP enträtselt hat, wird schnell zu Ruhm unter den Kryptographen kommen. Er wird viel Beifall ernten und eine Menge Geld angeboten bekommen.

  3. Die PGP Programmierer werden es sofort bekanntgeben.

Fast täglich verbreitet jemand eine Nachricht, wie "PGP durch Jugendlichen aus Omaha geknackt". Bezweifle diese Aussagen. Die Welt der Kryptographie zieht Paranoiker, Provokateure und Aliens in ihren Bann.

Bis heute hat niemand öffentlich vorgeführt, PGP überlistet oder geknackt zu haben.

Unterschied zwischen PGP und GnuPG

PGP ("Pretty Good Privacy") ist ein Produkt aus den USA und unterliegt der amerikanischen Gesetzgebung, beispielsweise den Exportbeschränkungen. Somit ist es in Europa nicht für alle Einsatzgebiete geeignet.

PGP wird zwar derzeit mit Quelltext ausgeliefert, aber dieser Quelltext ist nicht vollständig, und es gibt keine Garantie, daß dies auch in Zukunft so bleiben wird. PGP ist daher keine freie Software.

Desweiteren unterstützen aktuelle Versionen von PGP Optionen zur Einrichtung von Drittschlüsseln. Viele Anwender haben dadurch das Vertrauen in diese Software verloren.

GnuPG bietet de facto alle gängigen Verschlüsselunsmethoden an, die auch PGP bietet. GnuPG untersteht der GNU Public License (mehr Information im Internet unter http://www.gnu.org), dh.:

Einsatz von SSH (Secure Shell)

In Anlehnung an die SSH-FAQ40 soll ein Überblick über den Einsatz und die Technik von SSH gegeben werden.


Das Problem

Alles, was ein Rechner ins Netz schickt, kann prinzipiell von allen anderen Rechnern im gleichen Netzsegment gelesen werden. Das ergibt sich aus der Funktionsweise von Ethernet. Im Fall der Wohnheimnetze umfaßt das Netzsegment alle Rechner im HaDiKo, Waldhornstraße und Wachterbau. Selbstverständlich ist das Abhören fremder Daten per Benutzerordnung verboten, technisch verhindern läßt es sich aber mit der derzeit eingesetzten Netztechnik nicht.

Daher muß man sich bei der Benutzung von Netzdiensten Gedanken machen, welche Gefahren die Abhörbarkeit mit sich bringt. Besonders kritisch in dieser Hinsicht sind jede Art von Passwörtern: wer sich in den Besitz eines gültigen Accountname/Passwort-Paars bringt, kann damit auf fremden Rechnern beliebigen Unfug treiben, für den sich der legitime Inhaber des Accounts dann am Ende noch verantworten muß. Ein normales Telnet, FTP mit Passwort und andere Standarddienste übertragen immer Passwörter im Klartext und stellen damit ein beträchtliches Risiko dar.

Es sollte deswegen ein vorrangiges Ziel sein, niemals Passwörter im Klartext über das Netz zu senden.Dieses Ziel läßt sich mit passender Software erreichen. Grundsätzlich sind folgende Möglichkeiten dafür denkbar:

  1. Verwendung von Einmalpasswörtern;

  2. Authentifizierung mit Challenge-Response-Verfahren;

  3. Verschlüsselung des gesamten Datenverkehrs.

Methode (1) ist sehr unbequem zu benutzen und benötigt spezielle Login-Programme etc. Sie wird hier nicht weiter betrachtet.
(2) und (3) hängen eng zusammen, da teilweise die gleichen Verfahren verwendet werden. Verschlüsselung des gesamten Traffics ist allgemeiner und schützt auch gegen Ausspähen der Nutzdaten.
Ein spezieller, in letzter Zeit bekannt gewordener Angriff erlaubt es unter bestimmten Bedingungen, eine bestehende Verbindung (z.B. Telnet-Login) auf einen anderen Rechner umzuleiten. Diese Bedingungen sind im Wohnheimnetz erfüllbar. Dagegen schützt nur Methode (3).

Das Softwaresystem ssh(Secure Shell) implementiert die Methoden (2) und (3). Seine Verwendung ist auf allen Rechnern, wo die Software verfügbar ist (momentan Unix, OS/2, Amiga, Macintosh und Windows), dringend angeraten. Auf den Unix-Rechnern von Uni-Rechenzentrum und IRA ist ssh normalerweise standardmäßig installiert.

ssh bietet hinreichend allgemeine Möglichkeiten, um die meisten Netzdienste über verschlüsselte Kanäle ablaufen zu lasssen. Bei richtiger Konfiguration und konsequenter Anwendung ist es möglich, einen Rechner am Netz so zu betreiben, daß kein unverschlüsseltes Paket mehr den Rechner verläßt. (Abgesehen von nicht sicherheitsbedenklichen Daten wie Nameserveranfragen, etc.)


Beschreibung von ssh

ssh ist als "plug-in-compatible" zu den Standard-Unix-Programmen rsh und rlogin konzipiert. Mit diesen kann man sich auf anderen Rechnern einloggen oder direkt Programme starten. Dabei muß man kein Passwort eingeben, wenn auf dem Zielrechner konfiguriert ist, von welchen IP-Adressen Verbindungen angenommen werden. Das ist sehr bequem, aber IP-Adressen sind generell fälschbar und damit zur Authentifizierung nicht geeignet.

Daher bietet ssh eine Reihe von Sicherheitsmechanismen, mit denen diesem Problem abgeholfen wird. Neben der Verschlüsselung des gesamten Datenstroms mit Stromchiffren werden Hosts und User mit dem RSA-Verfahren23 durch public keys abgesichert.

Authentifizierungsverfahren

ssh bietet mehrere Möglichkeiten, wie sich der Benutzer dem Server gegenüber authentifiziert. Relevant sind insbesondere die Methoden "PasswordAuthentication" und "RSAAuthentication".

Passwort:

Dieses Verfahren wird dann verwendet, wenn eine Authentifizierung mit anderen Methoden nicht klappt. Dabei fragt der ssh-Client das Userpasswort in konventioneller Weise ab, schickt es aber verschlüsselt zum Server. Der Server wiederum behandelt das Passwort in der gewohnten Weise. Damit ist das Verfahren genauso zu handhaben wie telnet, aber sicherer - kein Abhören möglich.

RSA23:

Wirklich interessant ist die RSA-Authentifizierung. Dabei wird der RSA-Public-Key-Algorithmus verwendet: der Benutzer besitzt einen geheimen Schlüssel und der Host, auf dem er sich einloggen will (Zielhost) den dazugehörigen öffentlichen Schlüssel. Wie bei der Verifikation einer PGP-Signatur kann der Server feststellen, ob der geheime Schlüssel stimmt, ohne daß direkt brauchbare Klartextdaten übertragen werden. Es ist möglich, mit einem geheimen Schlüssel Zugriff auf mehreren Accounts zu erlauben, indem man den öffentlichen Schlüssel kopiert. Das macht das Verfahren sehr bequem in der Handhabung - ein Passwort muß weder gemerkt noch eingegeben oder regelmäßig geändert werden, es sei denn der geheime Schlüssel ist selber passwortgesichert.

Die Handhabung erfolgt so: zuerst erzeugt man sich mit dem Programm ssh-keygenein Schlüsselpaar. Das wird (auf Unix-Systemen) normalerweise in den Dateien ~/.ssh/identityund ~/.ssh/identity.pubgespeichert. Letzteres ist der öffentliche Schlüssel. Er hat die Form einer Textdatei, die aus einer langen Zeile besteht.

Auf jedem Zielhost kopiert man jetzt die identity.pub-Datei in ~/.ssh/authorized_keys. Ein Schlüssel muß genau eine Zeile sein, ggf. automatischen Zeilenumbruch im Editor deaktivieren. Der geheime Schlüssel darf natürlich nicht kopiert werden! Ein öffentlicher Schlüssel in authorized_keysbedeutet: Erlaube dem Inhaber des zugehörigen geheimen Schlüssels Zugriff auf diesen Account. Die Erlaubnis wird widerrufen, indem man die Zeile mit dem öffentlichen Schlüssel löscht.

Mit ssh-keygenkann der geheime Schlüssel zusätzlich passwortgeschützt werden. Dann muß man die hier definierte "Passphrase" bei jedem Zugriff auf den geheimen Schlüssel eingeben. Das ist wiederum unbequemer, aber schützt davor, daß der geheime Schlüssel in falsche Hände gerät.

Wenn ein geheimer Schlüssel unberechtigt kopiert wurde oder auch nur der Verdacht besteht, ist es - anders als bei PGP - ohne Umstände möglich, einen neuen anzulegen. Man muß nur darauf achten, daß man den alten öffentlichen Schlüssel aus allen authorized_keys-Files entfernt.

Filetransfer

ssh bietet das Kommando "scp" als plug-in-compatible zu rcp an. Damit lassen sich Files einfacher als mit FTP zwischen zwei Rechnern kopieren, wobei automatisch ssh verwendet wird. Anwendung wie in diesen Beispielen:

scp -p *.html rzstud1:.public_html

scp s_newuser@iraul1.ira.uka.de:perl-examples.ps ./misc

Weitere Erläuterungen sind in der Manpage.

TCP-Portumlenkung

Gleichzeitig mit der Login-Funktion arbeitet ssh auch als TCP-Proxy. Beim Aufruf des ssh-Befehls kann man beliebig angeben, daß TCP-Verbindungen auf bestimmten Ports der einen Seite auf Verbindungen auf der anderen Seite umgelenkt werden sollen. Dabei kommt zwischen beiden wiederum ein verschlüsselter Kanal zum Einsatz.

Eine solche Umlenkung wird mit den Kommandozeilenoptionen -Lbzw. -Rim ssh-Aufruf aktiviert. Dann passiert folgendes:

-Lport1:host:port2

Verbindungen auf den Port port1des Clients werden vom Server auf den Port port2des Hosts host vorgenommen

-Rport1:host:port2

Verbindungen auf den Port port1des Servers werden vom Client auf den Port port2des Hosts host vorgenommen

Ein Beispiel: mit

ssh rzstud1 -L9876:mailhost.rz.uni-karlsruhe.de:25

erreicht man folgendes: bei jedem Verbindungsaufbau auf Port 9876 des Client-Rechners wird rzstud1 eine Verbindung auf Port 25 (SMTP) des Mailhosts aufbauen und mit dem Client-Rechner koppeln. Das bedeutet, wer auf Port 9876 des Clients connected, bekommt eine SMTP-Verbindung zum Mailhost, die zwischen dem Client und rzstud1 verschlüsselt abläuft (zwischen rzstud1 und Mailhost dann unverschlüsselt). Dabei sieht der Mailhost allerdings nur rzstud1 als seinen Client. Weitere Anwendungsbeispiele finden sich unten.

X11 über ssh

Ein Sonderfall ist in ssh fest eingebaut, der die Bedienung sehr bequem macht: wenn man ssh aus einer X11-Session aufruft (DISPLAY ist gesetzt), dann wird eine Umlenkung für X11 aktiviert und gleichzeitig auf dem Zielhost DISPLAY und xauth passend gesetzt. Damit ist ohne weiteres Zutun der Aufruf von X11-Programmen sofort möglich, und das richtige Display wird benutzt.

Es ist zu empfehlen, X11-Verbindungen nur über ssh laufen zu lassen und niemals DISPLAY unbesehen umzusetzen, da das X11-Protokoll sehr unsicher ist. Niemals sollte man mit xhostZugriff auf ein Display erlauben. X-Displays sollten immer so konfiguriert werden, daß sie mindestens "Magic Cookie"-Autorisierung verwenden.Das gilt auch außerhalb der Wohnheimnetze.

Konfiguration

Un*x-Client

In der Datei /etc/ssh_configfinden sich Parameter für ssh. Das meiste, was standardmäßig eingestellt ist, funktioniert so. Man kann allerdings etwas optimieren. Ich verwende folgende Einstellungen:

# Site-wide defaults for various options


Host *

ForwardAgent no

ForwardX11 yes

RhostsAuthentication no

RhostsRSAAuthentication no

RSAAuthentication yes

PasswordAuthentication yes

FallBackToRsh no

UseRsh no

IdentityFile ~/.ssh/identity

Port 22

Cipher blowfish

EscapeChar none

KeepAlive no


Damit wird einiges, was ich nicht brauche, z.B. die rhosts-Authentikation, oder was ich unter keinen Umständen haben will (FallBackToRsh) gar nicht erst versucht. Als Verschlüsselung sollte man "blowfish" wählen, das ist am schnellsten. "arcfour" ist in neueren ssh-Versionen wegen eines potentiell die Sicherheit gefährdenden Fehlers deaktiviert.

Vor(!) dieser Defaulteinstellung können hostspezifische Optionen stehen, z.B. abgekürzte Hostnamen, Usernamen...:


Host rzstud1

HostName rzstud1.rz.uni-karlsruhe.de

IdentityFile ~olaf/.ssh/identity

User uknf


Ansonsten lese man sich die Manpage zu ssh durch, da ist eigentlich alles Notwendige zu finden.


Un*x-Server

Wer die Möglichkeit haben will, sich von außen (von anderen Rechnern im Netz oder auch aus der Uni) auf seinem eigenen Rechner einzuloggen, sollte den sshdaus einem der zahlreichen Initialisierungs-Skripts starten. Ich empfehle, ihn direkt nach dem inetdeinzutragen, da paßt er systematisch hin.

Analog zum Client gibt es auch für den ssh-Server eine Konfigurationsdatei /etc/sshd_config. Die sieht bei mir so aus:


# This is ssh server systemwide configuration file.


Port 22

ListenAddress 0.0.0.0

HostKey /etc/ssh_host_key

ServerKeyBits 768

LoginGraceTime 600

KeyRegenerationInterval 7200

PermitRootLogin yes

QuietMode no

FascistLogging no

PrintMotd yes

SyslogFacility AUTH

RhostsAuthentication no

RhostsRSAAuthentication yes

RSAAuthentication yes

PasswordAuthentication yes


Wichtig: RhostsAuthentication unbedingtauf "no" stellen. Außerdem im /etc/inetd.confden telnetd, rlogind, rshd und rexecd (und auch den ftpd, es sei denn, man betreibt einen Anonymous-FTP-Server) auskommentieren. Diese nehmen Passwörter im Klartext über das Netz an.

Weitere Informationen gibt es auch im SSH-FAQ.


Verwendung von normalen Netzdiensten mit ssh

Sämtliche Netzdienste, die eine Benutzeridentifikation mit Passwort benötigen, sollten nur über eine ssh-Verbindung benutzt werden. Das ist gar nicht schwer, sobald man es verstanden hat.

POP

(Bitte diesen Abschnitt auch lesen, wenn man selber kein POP verwendet, da die grundlegende Technik der Portumlenkung an diesem Beispiel erläutert wird.)

Mail mit POP zu verarbeiten, ist bequem und daher recht beliebt (und in den Standard-Mailprogrammen mancher Systeme eingebaut), stellt aber ein erhebliches Sicherheitsproblem dar. POP verlangt die Angabe des eigenen Account-Passwortes, das im Klartext übertragen wird (abgesehen davon, daß die Mail selber ebenfalls im Klartext durchs Netz geht). POP arbeitet auf einer einzelnen TCP-Verbindung zu einem bekannten Port und ist dadurch sehr einfach mit ssh zu sichern, so daß dieses Problem nicht mehr auftritt. Mit folgendem Befehl:

ssh rzstud1 -L110:poprzstud:110

wird eine Portumlenkung auf dem lokalen Rechner aktiviert. Der Parameter -La:b:csagt dem ssh-Client, daß jede Verbindung auf den Port a der lokalen Maschine auf den Port c der Maschine b weitergeleitet werden soll. Im Beispiel bedeutet das also, daß der lokale Port 110 auf Port 110 (POP3) auf der Maschine poprzstudumgeleitet wird. Diese Weiterleitung benutzt einen verschlüsselten Kanal.

Da man jetzt den lokalen POP-Port so belegt hat, daß Zugriffe darauf auf den POP-Port der rzstud1 weitergeleitet werden, kann und sollte man localhostals POP-Server konfigurieren. Dann muß man allerdings immer den oben genannten ssh-Befehl laufen haben, während man seine Mail liest - wenn er beendet wird, wird auch die Portumlenkung beendet.

Das gleiche Verfahren funktioniert mit allen Diensten, die auf einer einzigen TCP-Verbindung zu einer bekannten Portnummer basieren, also allen, die prinzipiell auch mit "telnet host port" angesprochen werden können. Beispiele für diese Dienste sind SMTP, aber auch telnet (als Notnagel für Maschinen, die noch keinen sshd haben).

Da die Umlenkung über einen Uni-Rechner läuft, kann es sich dabei auch um Maschinen außerhalb der Uni handeln. Mehr zu diesem Thema weiter unten.

Nicht-anonymes FTP

FTP paßt leider nicht in das im letzten Absatz beschriebene Schema, da für einen FTP-Transfer mehrere Verbindungen auf vorher nicht bekannten Nummern geöffnet werden müssen. Anonymes FTP enthält genau wie normale WWW-Zugriffe per se erst einmal keine kritischen Daten; relevant wird das aber bei Zugriffen mit Passwort, wie beim Transfer von Daten zwischen lokalem Rechner und Uni-Account.

Hierzu ist die beste Methode, ganz auf FTP zu verzichten und scp aus dem ssh-Paket zu benutzen, wo immer möglich. Eine allgemeine Lösung für FTP gibt es leider nicht. Als Notnagel könnte man SOCKS über ssh benutzen (s.u.), dann aber auch innerhalb der Uni! Ein HTTP-Proxy sollte für diesen Zweck ebenfalls nicht verwendet werden: das Passwort ist Bestandteil der URL und landet im Logfile des Proxy-Servers...

Sonstige

Mail verschickt wird mit SMTP (Port 25). Jede Mail, die wirklich niemand mitlesen soll, sollte eigentlich mit PGP verschlüsselt werden. Zumindest innerhalb des Wohnheimnetzes läßt sich aber das Mitlesen auf dem Netz mit einer ssh-Umlenkung des SMTP-Ports auf den Uni-Mailserver (nicht den HaDiKo-Mailserver!) verhindern.

Manche per HTTP zu erreichenden Dienste brauchen die Eingabe eines Passworts oder sonstiger geheimer Daten. Dafür sollte man den betreffenden Host auf einen beliebigen lokalen Port umlenken und in der URL localhost:portstatt des Original-Hosts verwenden:

aus http://www.foo.com:80/path/doc.htmlwird

eine Umlenkung -L8765:www.foo.com:80und

die URL http://localhost:8765/path/doc.html

An diesem Beispiel wird die Funktionsweise der Portumlenkung besonders deutlich, wenn man sie sich als Abbildung vorstellt:


http:// www.foo.com : 80 /path/doc.html

||||||||||| ||

ssh -L 8765 : www.foo.com : 80

|| ||||

http:// localhost : 8765 /path/doc.html


Man sollte beachten, daß die Benutzung eines HTTP-Proxys für solche Dienste grundsätzlich nicht zu empfehlen ist, da der Proxy prinzipiell die Passwörter loggen kann.

Für httpssind diese Verrenkungen nicht erforderlich, das Protokoll verschlüsselt selber (wenn auch die hierzulande erhältliche Software dafür nicht allzu sicher ist, die verwendeten 40-Bit-Schlüssel lassen sich mit genügend vielen Rechnern in ein paar Stunden knacken, wenn man es darauf ankommen läßt).

Welche Dienste man sonst noch benutzt, bei denen Passwörter verwendet werden, sollte man selber wissen...


Anmerkungen

Selbstverständlich erlaubt ssh die Angabe von mehreren Portumlenkungen als -Lport:host:port-Argumente auf einer Kommandozeile. Das können ruhig viele sein, der zusätzliche Speicherbedarf fällt nicht ins Gewicht. Am einfachsten schreibt man sich den Aufruf in ein kleines Shellscript. Alternativ definiert man dafür im /etc/ssh_configeine Pseudosite und schreibt die zusätzlichen Argumente dort rein:

Host relayer

HostName rzstud1.rz.uni-karlsruhe.de

IdentityFile ~foo/.ssh/identity

User ufoo

LocalForward 110 poprzstud.rz.uni-karlsruhe.de:110

# und weitere LocalForwards. Syntax beachten: nur ein Doppelpunkt

Dann reicht ein "ssh relayer" als Aufruf.

Wenn auf der lokalen Seite Ports im "reservierten" Bereich (unterhalb von 1024) umgelenkt werden, muß man den ssh-Client als root aufrufen. Für jeden Port kann immer nur ein ssh-Prozess mit der Umlenkung aktiv sein, weitere ssh-Clients können aber ohne die -L-Parameter gestartet werden.

Bei neueren Versionen von ssh sind die lokal umgelenkten Ports nur von localhostaus erreichbar. Dies verhindert, daß andere Rechner im Netz die Umlenkung benutzen und damit ihre Identität hinter dem Inhaber der Umlenkung verstecken (und eventuellen Unfug ihm anlasten). Daher muß man z.B. als POP-Server localhostund nicht den eigentlichen Rechnernamen angeben. Wer mehrere Rechner hat und von allen diesen aus die Umlenkung nutzen will, muß ssh mit dem Parameter -gstarten und unbedingt mittels entsprechender Firewall-Regeln dafür sorgen, daß die umgelenkten Ports aus dem restlichen Netz nicht erreichbar sind.

Chipkarten

Chipkarten sind miniaturisierte IT-Komponenten, meist in der genormten Größe einer Kreditkarte. Sie haben Eingang ins tägliche Leben gefunden, gewinnen zunehmend an gesellschaftlicher Bedeutung. Die derzeit bekannteste Chipkarten-Anwendung ist die Telefonkarte, die ein Guthaben enthält, das beim Gebrauch der Chipkarte in einem Kartentelefon reduziert wird, bis das Konto erschöpft ist und die Chipkarte unbrauchbar wird. Weitere Anwendungsbereiche von Chipkarten sind z. B. die Chipkarte im bargeldlosen Zahlungsverkehr und die SIM-Karten, die in Handys Verwendung finden.

Von der Technik her sind reine Speicherchipkarten zur Aufnahme von Daten (meist in Halbleiter-Technologie oder optischer Speichertechnik) von solchen Karten zu unterscheiden, in die Mikroprozessoren und speichernde Bauteile integriert sind. Solche Prozessorchipkarten sind als Kleinstcomputer ohne Mensch-Maschine-Schnittstelle anzusehen. Ihre Verwendung bedarf also zusätzlicher technischer Systeme zum Lesen der gespeicherten Daten, zum Aktivieren der Funktionen der Mikroprozessoren und zum Beschreiben der Speicher.

Wichtige Funktionalitäten der Chipkarten sind:

Um diesen Anforderungen gerecht zu werden verfügen Chipkarten über Sicherheitstechnologien, die den Schutz der Daten vor Mißbrauch gewährleisten sollen. Dabei muß auf folgende Gefahren eingegangen werden:

Die Schutzfunktionen der Chipkarten-Software basieren auf den bekannten und teilweise standardisierten Algorithmen zur Verschlüsselung, Signatur und Generierung von Zufallszahlen. Dazu gehören symmetrische Verschlüsselungsalgorithmen wie DES, Triple-DES, IDEA und SC85 und asymmetrische Verfahren wie RSA, Signieralgorithmen wie DSS und RSA mit RipeMD160, Einwegfunktionen zur Berechnung des MAC und für das Hashing wie SHA und RipeMD160 sowie Zufallszahlengeneratoren. Auf die technische Realisierung soll an dieser Stelle nicht weiter eingegangen werden. Nähere Informationen dazu sind in der Quelle

http://www.tec.informatik.uni-rostock.de/RA/LfD-MV/ak_tech/tud/akt_chka.html

dargestellt.


Quellennachweis


[ALLGEMN]

http://www.thur.de/ulf/krypto/



[BEUTLSP]

Beutelspacher, Albrecht: Kryptologie. Braunschweig/Wiesbaden: Friedr. Vieweg & Sohn, 1996.


[CHIPCRD]

http://www.tec.informatik.uni-rostock.de/RA/LfD-MV/ak_tech/tud/akt_chka.html


[ENIGMA1]

http://www.geocities.com/CapeCanaveral/Hangar/4040/bombe.html



[ENIGMA2]

http://www.wadham.ox.ac.uk/~ahodges



[ENIGMA3]

http://www.unix-ag.uni-kl.de/~conrad/krypto/misc/enigma.html



[ENIGMA4]

http://www.cranfield.ac.uk/ccc/bpark/bombe.html



[ENIGMA5]

ftp://agn-www.informatik.uni-hamburg.de/pub/cryptsim/gifs



[GIESSMN]

Giessmann: Kryptologie SS96. TU-Berlin, Vorlesungsskript, 1996


[GNUPG1]

http://www.gnupg.de© GnuPG-Group



[KIPPHAN]

Kippenhan, Rudolf: Verschlüsselte Botschaften. Hamburg: Rowohlt Verlag, 1997. -ISBN 3 -498 -03495 -2


[KRPGSH1]

http://rhlx01.rz.fht-esslingen.de/projects/krypto/krypt_gesch/krypt_gesch.html


[KRPGSH2]

http://www.lexiter.com/misc/ps_crypto/highlights.html


[KRPGSH3]

http://rhlx01.rz.fht-esslingen.de/projects/krypto/krypt_gesch/krypt_gesch-2.html

[PGPFAQ1]

http://www.iks-jena.de/mitarb/lutz/security/Übersetzung © Lutz Donnerhacke

[PLAYFAR]

http://www.falcom.net/Kryptographie/playfair.html


[SGARRO]

Sgarro, Andrea: Geheimschriften. Augsburg: Weltbild, 1991. -ISBN 3-89350-162-2


[SSHFAQ1]

http://sites.inka.de/sites/bigred/hadinet/ssh.html © Olaf Tietz


[TRANSPO]

http://www.informatik.tu-muenchen.de/~gerold/aktvorl9899/transpos.htm