Deutsche Telekom AG - Fachhochschule Leipzig

Kryptologie

Fachbericht

Seminargruppe 99/1 - Projektgruppe A

Deutsche Telekom AG - Fachhochschule Leipzig

Kryptologie

Die Wissenschaft vom Ver- und Entschlüsseln

Angefertigt von: Höppner, Tobias, 99115

Lingel, Steve, 99121

Romeyke, Andreas, 99131

Schreiter, Michael, 99134

Beginn: 04.01.2000

Ende: 21.01.2000

Erstprüfer/Betreuer: Herr Hempel

Zweitprüfer/Betreuer: Frau Schindler

Inhalt

1 Zur Bedeutung der Kryptologie 1

2 Geschichtlicher Überblick 1

3 Grundlagen 2

3.1 Terminologie 2

3.2 Prinzipien von Kerckhoff 3

3.3 Prinzipien von Shannon 4

4 Geheimhaltung 5

4.1 Klassische Verfahren 5

4.1.1 Substitution 5

4.1.2 Transposition 6

4.1.3 Playfair-Chiffre 7

4.1.4 Vignère-Chiffre 8

4.1.5 Chiffrierzylinder 10

4.1.6 Rotormaschinen 10

4.2 Moderne Verfahren 12

4.2.1 Der DES-Algorithmus 12

4.2.2 Das RSA-Verfahren 13

5 Integrität und Authentizität 15

5.0 Einordnung 15

5.1 Integrität von Nachrichten 15

5.2 Benutzerauthentikation 16

5.3 Zero-Knowledge-Protokolle 17

6 Anwendungen 17

6.0 Motivation 17

6.1 PGP und GnuPG 18

6.2 SSH (Secure Shell) 19

6.3 Chipkarten 20

Anlagen 21 Quellennachweis 25

1 Zur Bedeutung der Kryptologie

Kryptologie spielt in unserer heutigen Zeit eine immer wichtiger werdende Rolle. Dies ist in dem Wandel von der Industrie- zur Informationsgesellschaft begründet. Täglich hat jeder von uns mit kryptologischen Technologien bewußt oder unbewußt zu tun. Sei es das bargeldlose Bezahlen mittels EC-Karte, das Benutzen von Kartentelefonen oder Handys, der Umgang mit Computern am Arbeitsplatz oder die Nutzung von Bezahl-Fernsehen (Pay-TV). Die Entwicklung und die Bedeutung der Kryptologie herauszustellen, sowie Anregungen für die tiefere Beschäftigung mit dieser Materie zu geben, soll das erklärte Ziel dieser Publikation sein.

2 Geschichtlicher Überblick

Tabelle 1: Zeittafel

3 Grundlagen

3.1 Terminologie

Zunächst einige Worte zur Terminologie. Die Begriffe Kryptologie und Kryptographie sind aus den griechischen Wörtern kryptos (geheim) logos (das Wort, der Sinn), und graphein (schreiben) gebildet. Meist wird mit Kryptologie die Gesamtheit der Kryptoanalyse und Kryptographie bezeichnet, wobei die Kryptographie sich mit der Verheimlichung von Nachrichten und die Kryptoanalyse mit dem Brechen von geheimen Nachrichten beschäftigt. Ein Klartext ist die Information, die der Empfänger erhalten soll. Ein Geheimtext ist ein verschlüsselter Klartext, das heißt für Andere nicht mehr lesbar. Den Vorgang der Verschlüsselung bezeichnet man auch als Chiffrierung, den der Entschlüsselung als Dechiffrierung. Die Begriffe Chiffre oder Code bezeichnen das Verfahren, das der Chiffrierung bzw. der Dechiffrierung zugrunde liegt. Die geheime Information, die zur Verschlüsselung und Entschlüsselung dient, nennt man Schlüssel. Wird zum Chiffrieren und Dechiffrieren der gleiche Schlüssel benutzt, so spricht man von einem symmetrischem Verfahren. Dem gegenüber gibt es Verfahren, bei denen zwei oder mehr Schlüssel verwendet werden, das heißt der Chiffrierschlüssel ist ein anderer, als der Dechiffrierschlüssel. Diese Verfahren sind asymmetrisch und werden auch als public-key-Verfahren bezeichnet. Die Kryptographie teilt sich grob in die drei Aufgabenbereiche der Geheimhaltung, Integrität und Authentizität auf, wobei sich letztere mit der Übertragungs- und Fälschungssicherheit beschäftigen. Aufgabe der Kryptoanalyse ist es, geheime Nachrichten ohne Kenntnis des Schlüssels lesbar zu machen. Man unterscheidet dabei den passiven Angriff, bei dem Nachrichten nur mitgelesen werden und den aktiven Angriff, bei dem der Inhalt verändert wird oder Nachrichten mit gefälschten Absendern übermittelt werden.

3.2 Prinzipien des Auguste Kerckhoff

Auguste Kerckhoff von Nieuwenhof geboren 1835 in den Niederlanden, studierte in Deutschland und lebte schließlich in Frankreich, wo er 1903 verstarb. Er schrieb unter anderem ein Buch zu Volapürük, einer künstlichen, Esperanto-ähnlichen Sprache. Er galt als einer der bedeutendsten Kryptographen der Telegraphenzeit und unterschied zwischen taktischen und strategischen Zielen der Geheimhaltung, also dem zeitweiligen Schutz und den zeitlosen Schutz der Nachricht und attackierte die bis dahin bei den Kryptologen gültige Formel „Melius est abundare quam deficere“ - „Lieber zuviel als zu wenig“. Er forderte, dass die Sicherheit ganz oder zumindest zu einem wesentlichen Teil vom Schlüssel abhängen muß. Auguste Kerckhoff beschreibt die Voraussetzungen für eine sichere Verschlüsselung folgendermaßen: "Ein Verfahren ist dann sicher, wenn man es nicht knacken kann, obwohl man den Code kennt." 1883 beschreibt Auguste Kerckhoff in seinem Buch 'La Cryptographie Militaire', die folgenden sechs Regeln, gewonnen aus seinen Studien der historischen Kryptographie, die jeder befolgen sollte, wenn er sein Geheimnis bewahren will:

• die verschlüsselte Nachricht sollte praktisch unknackbar sein,

• die Korrespondenten (Sender und Empfänger) dürfen keinen Schaden erleiden, wenn das Chiffriersystem geknackt wurde (zeitweiliger Schutz),

• der Schlüssel muß leicht auswendig zu lernen und veränderbar sein,

• die Kryptogramme müssen über Telegraphen übertragbar sein,

• der Chiffrierapparat und die Dokumente müssen leicht transportierbar sein,

• das System muß einfach zu benutzen sein, und sollte keine übermäßigen geistigen Anstrengungen verlangen,

• das Chiffriersystem sollte von Experten gut untersucht sein.

3.3 Prinzipien Shannons

Der amerikanische Mathematiker Claude Shannon, geboren 1916 gilt als der Vater der Informationstheorie. Unter anderem beschäftigte er sich auch mit künstlicher Intelligenz, sowie mit künstlichen Schachautomaten. In seinem Buch „Mathematical Theory of Communication“ revolutionierte er die Nachrichtentechnik genauso grundlegend, wie in seinem wissenschaftlichen Beitrag „Communication Theory of Secrecy Systems“, welchen er 1949 veröffentlichte und indem er seine kryptologischen Theoreme darstellte:

• Wenn man eine Chiffre mit nicht wiederverwendbaren Schlüssel zu Hilfe nimmt, so entspricht die Aufeinanderfolge der Buchstaben oder Ziffern, die das Kryptogramm zusammensetzen einer reinen Zufallsfolge (Bsp: abdccda ist zufällig, abcdabcd nicht).

• Wenn man eine Chiffre mit nicht wiederverwendbaren Schlüssel nimmt, so ergibt das Fehlen eines Schlüssels keinerlei Information über den Inhalt der Klartextbotschaft.

• Bei einem vollkommenen Chiffrierverfahren kann der Schlüssel nicht kürzer sein als der Klartext (Ein nicht wiederverwendbarer Schlüssel entspricht einer irrationalen Zahl).

Das theoretisch perfekte Kryptosystem ist, wenn man die Aussagen von Kerckhoff und Shannon zusammen nimmt, ein System, was einen nicht wiederverwendbaren Schlüssel besitzt und praktisch nicht knackbar ist, d.h. keinerlei Information über den Klartext zuläßt und damit gegen statistische Tests unanfällig ist. Ein Verfahren, das diese Annahmen erfüllt ist das 1917 von Vernam entwickelte „One-Time-Pad“, welches z.B. von Che Guevara benutzt wurde und auch heute noch den „heißen Draht“ zwischen Moskau und Washington sichert. Leider ist es sehr schwierig, alle Prinzipien unter einen Hut zu bringen wenn es um praktikablere Lösungen geht. Beim One-Time-Pad zum Beispiel ist der Schlüssel viel zu lang, oder die Erzeugung von Zufallsfolgen macht Probleme. Doch wenn man noch mal Kerckhoff zu Rate zieht, dann hat das Chiffriersystem seinen Zweck erfüllt, wenn es praktisch sicher ist, bis die Information, die geheimgehalten werden sollte, durch die Zeit wertlos geworden ist.

4 Geheimhaltung

4.1 Klassische Verfahren

4.1.1 Substitutionsverfahren

Die Grundidee dieser Gruppe von Verfahren ist es, die Buchstaben des Klartextes mit Hilfe einer Zuordnungstabelle durch andere Symbole zu ersetzen. Diese Symbole können Sonderzeichen, Buchstaben oder Zahlen sein. Man unterscheidet monoalphabetische Chiffren, bei denen der gesamte Text mit einer festen Zuordnungstabelle verschlüsselt wird und polyalphabetische Chiffren, die mehrere Zuordnungstabellen im Wechsel verwenden. Im folgenden werden verschiedene praktisch verwendete monoalphabetische Chiffren erläutert. Der Vigenère- und der Playfair-Chiffre als Repräsentanten für polyalphabetische Chiffren werden weiter unten dargestellt.

Tabelle 2: Allgemeine Substitution

Klartext: MEIN NAME IST HASE

Geheimtext: ZIXR RLZI XJK ULJI

Eines der bekanntesten klassischen Verschlüsselungsverfahren wurde nach Cäsar benannt. Dieser benutze es für den Briefwechsel mit seinen Statthaltern, Generälen und Konsuln. Die Nachricht wird verschlüsselt indem man jeweils eine bestimmte Anzahl von Buchstaben im Alphabet weitergeht. Der Schlüssel ist dabei die Angabe, welcher Geheimtextbuchstabe dem A entspricht z.B. A=D

Tabelle 3: Cäsar-Chiffre A=D

Klartext: PROJEKT MACHT SPASS

Geheimtext: SURMHNW PDFKW VSDVV,A=D

Die Substitutionsmethode mit A=N ist eine Sonderform des Cäsar-Codes. Sie zeichnet sich dadurch aus, dass die Zuordnung der Buchstaben symmetrisch ist, d.h. (A=N, N=A usw.). Dieses Verfahren ist auch als ROT13-Verfahren bekannt, weil die Buchstaben um 13 Stellen rotiert werden.

Tabelle 4: ROT13-Codetabelle

Ein sehr altes Verfahren ist das um 600 v.Chr. in Palästina angewandte Atbash-Verfahren, bei dem das Schlüssel-Alphabet in umgekehrter Reihenfolge dem Klartextalphabet zugeordnet wurde.

Tabelle 5: Atbash-Codetabelle

4.1.2 Transpositionsverfahren

Beim Transpositionsverfahren werden die Zeichen des Klartextes nicht durch andere ersetzt, sondern lediglich in der Reihenfolge vertauscht.

Grundprinzip

Als Grundlage dient eine Matrix in die das zu chiffrierende Wort zeilenweise eingetragen wird. Die Anzahl der Spalten ist der geheime Schlüssel. Daraus und aus der Gesamtlänge des Klartextes ergibt sich die Anzahl der Zeilen in der Matrix. Das Chiffre wird durch spaltenweises Auslesen der Matrix gebildet. Das noch im Jahr 1917 vom deutschen Heer eingesetzten Drehraster basierte auf diesem Verfahren.

Beispiel: Matrix mit Schlüssel 6

Tabelle 6: Allgemeine Transpsitionsmatrix

spaltenweise ausgelesen: IDTECEONHRRBBDEAIOIRNKST

Spalten-Transposition

Alternativ dazu kann man die Matrix auch nach einer vorgegebenen Permutation spaltenweise auslesen. Zur Erhöhung der Sicherheit kann man das Ergebnis erneut in die Matrix einschreiben und auslesen.

Beispiel: Schlüssel: 4 Auslesepermutation: 3421

Tabelle 7: Spaltentransposition

permutiert ausgelesen: WCDE AHUL SSNK ERON

Gemischte Zeilen- und Spalten-Transpositionen

Bei dieser Abwandlung des Verfahrens wird nicht nur das Auslesen, sondern auch das Einschreiben in die Matrix permutiert.

Bsp.: Schlüssel: 4

Einschreibepermutation der Zeilen: 2413

Auslesepermutation der Spalten: 2143

Tabelle 8: Gemischte Zeilen- und Spaltentransposition

Geheimtext: 6 14 2 10 5 13 1 9 8 16 4 12 7 15 3 11

Dechiffrierung

Mit der Kenntnis des Schlüssels, des verwendeten Algorithmus und der Länge des Geheimtextes kann die Matrix wiederhergestellt und rückwärts ausgelesen werden. Dabei erhält man den Klartext zurück. Ohne Kenntnis des Schlüssels muß man auf Kryptoanalyse zurückgreifen. Dabei versucht man, aus Zeichenhaufen sinnvolle Kombinationen (Anagramme) zu bilden. Eine weitere Hilfe ist das Aufstellen von Häufigkeitsstatistiken (z.B. Bigramme, Trigramme), wenn der Klartext einer natürlichen Sprache entstammt.

4.1.3 Playfair-Chiffre

Die Playfair-Verschlüsselung wurde in diplomatischen Kreisen und vor allem beim Militär verwendet, zum Teil heute noch. In beiden Weltkriegen war dieser Algorithmus durch seine einfache Handhabung weit verbreitet. Der Algorithmus beruht auf der Verschlüsselung von Buchstabengruppen, nicht von einzelnen Zeichen, dadurch wird die Häufigkeit verschleiert. Als Grundlage dient eine 5*5 Matrix.

Tabelle 9: Playfair-Quadrat

Das Schlüsselwort, in diesem Fall „Gruenspan“ wird eingetragen, und sich wiederholende Buchstaben werden weggelassen. Anschließend werden die restlichen Buchstaben des Alphabetes der Reihe nach eingetragen. I und J teilen sich ein Feld, was jedoch kaum Nachteile bringt.

Der Verschlüsselungsvorgang

Der Klartext wird in Zweiergruppen zerlegt. Bei doppelten Buchstaben muß ein vereinbartes Zwischenzeichen eingefügt werden z.B. X. Diese Zweiergruppen werden nun nach folgendem Schema chiffriert. Liegen beide Buchstaben in einer Zeile der Matrix, werden jeweils die beiden Zeichen rechts davon als Chiffre notiert. Liegen sie in ein und derselben Spalte werden jeweils die beiden Zeichen darunter notiert. Wenn ein Paar weder in der gleichen Zeile noch in der gleichen Spalte liegt notiert man jeweils den Buchstaben, der in der Zeile des ursprünglichen und in der Spalte des zweiten Buchstaben steht.

Beispiel:

die katze trat die treppe krumm => Zerlegung in Zweiergruppen

DI EK AT ZE TR AT DI ET RE PX PE KR UM MX => Buchstabenpaare in Matrix suchen

aus DI wird FK, aus EK wird NI usw. Es entsteht:

FK NI CO YN NM CO FK QN UN AW BR FN RO OW

Der Entschlüsselungsvorgang

1. Text in Zweiergruppen einteilen

2. Matrix mit richtigem (aktuellem) Schlüsselwort benutzen

3. Zweiergruppen rückwärts verschlüsseln

Die Sicherheit

Im Playfair-Chiffre fallen häufig auftretende Buchstaben nicht mehr so auf, dafür treten die Bigramme mehr in den Vordergrund, deren Wahrscheinlichkeitsverteilung aber ausgeglichener ist. Der Ansatz für die Kryptoanalytiker ist, daß jedes Zeichen nur 5 verschiedene Bilder hat, die 4 in seiner Zeile und das Zeichen unter ihm. Häufige Buchstabengruppen, z.B. ER, EN, TE stehen neben oder in der Zeile des E’s. Der Vorteil dieses Verfahrens ist es, dass mit einer Teilentschlüsselung noch nicht der gesamte Klartext erschlossen werden kann.

4.1.4 Vigenère-Chiffre

Die Vigenère-Verschlüsselung ist die bekannteste unter allen polyalphabetischen Algorithmen. Sie wurde im Jahre 1586 von dem französischen Diplomaten Blaise de Vigenère (1523 bis 1596) der Öffentlichkeit zugänglich gemacht. Der Hauptgedanke dieser Methode ist, verschiedene monoalphabetische Chiffrierungen im Wechsel zu benutzen. Zur Chiffrierung der Nachrichten nach dem Algorithmus von Vigenère braucht man unbedingt ein Schlüsselwort und das Vigenère-Quadrat [siehe Anlage 1]. Ohne Schlüsselwort kann man nicht sagen, welche Geheimtextzeichen den Klartextzeichen entsprechen. Dabei kann das Schlüsselwort jede beliebige Buchstabenfolge sein. Um diese Verschlüsselungsmethode zu demonstrieren nehmen wir ein Beispiel. Wir wählen ein beliebiges Schlüsselwort, z.B. "HALLO" und schreiben dieses Wort zeichenweise über den Klartext, und zwar so lange, bis die Länge des Klartextes erreicht ist: 

Schlüsselwort:      H A L L O H A L L O H A L
Klartext:           k r y p t o g r a p h i e
Geheimtext:         R R J A H V G C L D O I P 

Das Schreiben des Geheimtextes ist wie folgt zu erklären: Der über einem bestimmten Klartextzeichen stehende Schlüsselwortbuchstabe und der direkt darunterliegende Klartextbuchstabe bestimmen anhand des Vigenère-Quadrates das Chiffre-Alphabet, mit dem der Klartextbuchstabe zu verschlüsseln ist. Den ersten Geheimtextbuchstaben „R“ bekommen wir, wenn wir im Vigenère-Quadrat in der Zeile „H“ und der Spalte „k“ nachschauen. Weiter suchen wir in der Zeile „A“ den Buchstabe in der Spalte „r“; dieser ist ebenfalls ein „R“. (Das ist nur ein Zufall, dass zwei gleiche Geheimtextbuchstaben hintereinander stehen.) In gleicher Weise führen wir die Verschlüsselung weiter durch.

Angriffspunkte für die Kryptoanalyse - der Kasiski-Test

1863 stellte der preußische Infanteriemajor Friedrich Wilhelm Kasiski erstmals ein Verfahren zur systematischen Analyse und Dechiffrierung von mit Vigenére verschlüsselten Botschaften dar. Das Verfahren stützt sich darauf, dass sich ein im Verhältnis zur Textlänge relativ kurzes Schlüsselwort ständig wiederholt. Dadurch kann es auftreten, dass zwei gleiche Wörter des Klartextes auch im verschlüsselten Text gleich sind. Dies ist immer dann der Fall, wenn der Abstand zwischen diesen Wörtern ein Vielfaches der Schlüsselwortlänge ist. Bei einem 5 Buchstaben langen Schlüsselwort würden also zwei gleiche Wörter im Abstand von 5, 10, 15, 20, ... Buchstaben gleich verschlüsselt werden. Kasiski ging nun so vor, dass er sich im verschlüsselten Text möglichst lange Buchstabenkombinationen suchte, die mehrfach auftraten und den Abstand dazwischen zählte. Diese ermittelten Abstände sind ein Vielfaches der Schlüsselwortlänge. Diese Vorgehensweise läßt sich recht einfach automatisieren, indem man den verschlüsselten Text gegen sich selbst verschiebt und die Übereinstimmung der Buchstaben zählt. Ist die Verschiebung gleich oder ein Vielfaches der Schlüsselwortlänge tritt eine markant hohe Übereinstimmung auf [siehe Anlage 2]. Weiß man nun die Schlüssellänge kann man den Text sortieren nach Buchstaben, die mit dem selben Schlüsselbuchstaben verschlüsselt wurden. Bei der Schlüssellänge 5 nimmt man also den 1., 6., 11.,... in eine Gruppe, dann den 2., 7., 12., ... usw. Diese einzelnen Gruppen kann man nun statistisch analysieren. Man braucht dabei nur ein Klartext-Chiffre-Buchstabenpaar zu finden, da alle Buchstabe in einer Gruppe um den selben Wert verschoben sind. Man sucht also z.B. nach dem E, welches in den europäischen Sprachen der häufigste Buchstabe ist. Findet man nun z.B. in einer Gruppe das H am häufigsten auf, kann man davon ausgehen, dass diese Gruppe um 3 Stelle verschoben ist (Schlüssel=Kryptogramm-Klartext; H-E=D) Der Schlüsselbuchstabe dieser Gruppe ist also D. Dasselbe macht man mit allen Gruppe und erhält so das Schlüsselwort.

4.1.5 Chiffrierzylinder

Der Chiffrierzylinder stellt eine erste Mechanisierung der polyalphabetischen Substitution dar. Er besteht aus mehreren Scheiben, die auf einer Achse drehbar gelagert sind. Auf den Außenrändern der Scheiben sind permutierte Alphabete eingraviert, d.h. Alphabete in willkürlichen Reihenfolgen. Jede Scheibe enthält eine andere Permutation. Hat man beispielsweise 20 solcher Scheiben, dreht man diese so gegeneinander, dass in einer Zeile 20 Zeichen des Klartextes eingestellt sind. Den Geheimtext kann man nun in einer beliebigen Zeile ablesen. Zum Dechiffrieren wird der Geheimtext in einer Zeile eingestellt und der Klartext in einer anderen Zeile gesucht. Der Schlüssel ergibt sich aus der Anordnung der Scheiben, das sind bei 20 Scheiben 20! oder 2,4*10¹⁸ Möglichkeiten.

4.1.6 Rotormaschinen

Hierbei handelt es sich um elektromechanische Verschlüsselungsgeräte, die aus Rotoren bestehen. Rotoren sind dicke, elektronisch isolierte Scheiben, auf denen auf den gegenüberliegenden Flächen je 26 Schleifkontakte ringförmig angebracht sind. Dabei stellt jeder Schleifkontakt einen Buchstaben des Alphabetes dar. Jeder Kontakt der linken Seite ist genau mit einem Kontakt der rechten Seite verbunden. Man erhält eine einfache Substitution. Legt man an einen der linken Schleifkontakte eine Spannung an, gelangt diese zu einem der rechten Kontakte und bringt eines von 26 Lämpchen zum Leuchten. Das aufleuchtende Lämpchen ist abhängig von der inneren Verdrahtung des Rotors. Dreht man nun den Rotor nach jedem Zeichen um eine Position weiter, erhält man eine polyalphabetische Substitution mit der Periode 26. Zur Erschwerung der Kryptoanalyse benutzt man statt einer, mehrere hintereinander liegende Scheiben, die über ihre Schleifkontakte miteinander verbunden sind.

Dabei hat jede der Scheiben eine andere innere Verdrahtung.

Die Enigma

Das Wort Enigma stammt aus dem Griechischen und bedeutet soviel wie „Rätsel“. Die Enigma ist der berühmteste Vertreter der Rotormaschinen. Sie wurde im Jahr 1923 von Arthur Scherbius gebaut. Die ersten Modelle waren normale Rotormaschinen mit 4 Rotoren und wurden seit dieser Zeit von der deutschen Wehrmacht für den Funkverkehr verwendet.

Aufbau der Enigma

Im Jahr 1926 veränderte Willi Korn den Aufbau der Enigma. In seiner Konstruktion benutzt Korn nur noch 3 Rotoren, die aber einen beweglichen Ring hatten, auf dem die Zahlen 1 bis 26 (das Alphabet) aufgedruckt waren. Durch diesen Ring konnte nun die innere Verkabelung in bezug auf die äußere Numerierung geändert werden. Dadurch vergrößerte sich der Schlüsselraum. Eine weitere Neuerung war ein vierter Rotor, welcher auch als Reflektor bezeichnet wird. Dieser hatte nur auf einer Seite Schleifkontakte, von denen jeder mit einem anderen fest verdrahtet war. Der Reflektor befand sich fest an der äußeren rechten Seite und sollte die von links kommenden Signale auf einem anderen Weg zurück nach links senden. Durch den Reflektor konnte kein Zeichen auf sich selbst abgebildet werden. Außerdem waren nun Codierung und Decodierung gleich, d.h. das für die Codierung exakt die selbe Ausgangsstellung benutzt werden mußte, wie sie bei der Codierung verwendet wurde. Weiterhin wurde ein Steckfeld eingeführt, über welches die Buchstaben vor und nach der Ver- und Entschlüsselung vertauscht werden. Dazu mußte man eine Steckbrücke in die zu vertauschenden Buchstaben in das Steckfeld stecken. Die nicht gesteckten Buchstaben blieben unberührt.

Die letzte wichtige Neuerung war die Einführung einer Übertragungsfunktion. Sie arbeitete wie ein Kilometerzähler beim Auto. Nach der Eingabe eines Zeichens und der dazugehörigen Ausgabe des chiffrierten Buchstabens wurde der äußerst links stehende Rotor stets um eine Position weiter gedreht. Wenn er nun eine Position erreichte, die durch eine veränderbare Kerbe am Rotor markiert war und nun der Rotor noch einmal gedreht wurde, so führte die Mechanik gleichzeitig eine Drehung des linken, sowie des rechts neben ihm stehenden Rotors aus.

Die Enigma wurde später noch an einigen Stellen erweitert. So kamen im Laufe der Zeit immer weitere Rotoren hinzu. Gegen Kriegsende sollen es etwa 10 Stück gewesen sein. Laut Codebuch suchte man aus diesen 10 die richtigen 3 Rotoren aus, und setzte sie in die Maschine ein. 1942 wurde die Enigma der Marine um einen Rotor erweitert, so dass im Gegensatz zur Heeres-Enigma 4 statt 3 Rotoren zur Ver- und Entschlüsselung benutzt wurden. Der Schlüsselraum, etwa 2*10²⁰, ergibt sich aus der Anzahl der zur Auswahl stehenden Rotoren, der möglichen Ausgangsstellungen der Rotoren, der Initialpermutation und der verschiedenen Steckfeldanordnungen. Die Periode der Enigma mit 3 Rotoren beträgt 16900.

Zum Gebrauch der Enigma

Vor der Benutzung mußten folgende allgemeine Einstellungen vorgenommen werden:

• Auswahl der zu benutzenden Rotoren

• Reihenfolge der Rotoren

• rotorspezifische Einstellungen für Übertrag und Ringposition auf dem Rotor

• Kombinationen auf dem Steckfeld

Die Einstellungen waren durch Codebücher festgelegt. Die Codebücher waren immer auf einen Monat und jede Einstellung auf 24 Stunden begrenzt. Anschließend mußte man die Anfangspositionen der Rotoren, welche frei wählbar waren, einstellen. Diese Positionen wurden allerdings auch zum Dechiffrieren benötigt. Somit war es notwendig, dass die Anfangspositionen mit dem Geheimtext gesendet werden mußten.

Schwachstellen

Der für damalige Verhältnisse riesige Schlüsselraum veranlaßte die Verantwortlichen auf deutscher Seite, ihrer Maschine bedingungslos zu vertrauen. Sie hielten einen Einbruch in die Enigma für unmöglich.

Die gravierendste Schwachstelle der Enigma war wohl, dass sie auf einem käuflichen Chiffriergerät beruhte. Außerdem wurde sie in solch großer Anzahl benutzt, dass es unmöglich war, die innere Verdrahtung der Rotoren geheimzuhalten. Das wichtige Geheimnis um die innere Verdrahtung dürfte nur für neu entwickelte Rotoren bestanden haben, dieses aber auch nur für kurze Zeit. Desweiteren wurden zwar immer wieder Veränderungen der Enigma vorgenommen, welche jedoch nur halbherzig ausgeführt waren. Beispielsweise war der vierte Rotor der Marine-Enigma fest eingebaut. Wäre dieser wie die anderen Rotoren austauschbar gewesen, hätte sich der Schlüsselraum um den Faktor 234 statt 26 vergrößert.

Eine weitere Schwachstelle liegt in der Benutzung der Enigma. Wie bereits erwähnt waren die Grundeinstellungen über Codebücher festgelegt und somit für 24 Stunden bei allen Enigmamaschinen gleich. Dies erleichterte die Kryptoanalyse, wenn einmal die Tageseinstellungen bekannt waren, zum Beispiel über erbeutete Codebücher. Nun mußten bei allen Geheimtexten nur noch die Anfangsrotorpositionen ermittelt werden. Später sollen auch Codebücher mehrmals benutzt worden sein. Ein weiteres Problem war die Übertragung der Anfangsposition der Rotoren. Sie wurde als Klartext an den Beginn der zu übermittelnden Nachricht gestellt. Die typischen Armeenachrichten, welche oft kurz und gleichen Inhalts waren, stellten einen zusätzlichen Risikofaktor dar. Gute Kryptoanalytiker konnten aus ihnen Schlüsse auf den Klartext ziehen.

4.2 Moderne Verfahren

4.2.1 Der DES-Algorithmus

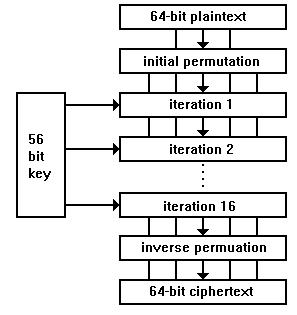
Der DES Algorithmus [siehe Anlage 4] ist ein Produktalgorithmus, speziell ein Feistel-Netzwerk. Er verwendet einen 56 Bit langen Schlüssel, um blockweise 64 Bit Klartext in 64 Bit Geheimtext zu überführen bzw. umgekehrt. Das geschieht in 16 schlüsselabhängigen Runden. Vor der ersten und nach der letzten Runde werden jeweils eine feste, bitweise Transposition durchgeführt. Dabei ist die abschließende Permutation die Umkehrung der ersten.

Aufbau der runden- und schlüsselabhängigen Funktion f von DES

[siehe Anlage 5]

Es werden 48 Bit, in Abhängigkeit der Runde des veränderten 56 Bit Schlüssels, ausgewählt. Die Rechte Blockhälfte wird von 32 auf 48 Bit erweitert. Beide 48 Bit-Folgen werden durch XOR verknüpft. Das Ergebnis wird mittels acht S-Boxen in eine 32 Bit-Folge transformiert. Jetzt wird die 32 Bit-Folge durch eine P-Box permutiert. Der entstandene 32 Bit Block braucht nun nur noch per XOR mit der linken Blockhälfte verknüpft zu werden und es ergibt sich die rechte Blockhälfte der neuen Runde. Die Dechiffrierung verläuft ganz ähnlich nur mit umgekehrter Reihenfolge der Rundenschlüssel ab.

Eingangs und Ausgangspermutation

Die Permutationen vor der ersten und nach der letzten Runde dienen keiner Sicherheit. Vermutlich liegt ihre Verwendung in der Hardware begründet, denn Mitte der 70er Jahre war es noch nicht so einfach, 64 Bit Daten in ein Register zu laden, es gab noch nicht einmal 16 Bit Mikroprozessoren.

4.2.2 Das RSA-Verfahren

RSA ist ein von Ron Rivest, Adi Shamir, Leonard Adleman entwickeltes asymmetrisches Public-Key-Verfahren. Es überstand eine jahrelange Kryptoanalyse und wird heute als Standardverfahren von fast allen gängigen Verschlüsselungssystemen eingesetzt. Bevor verschlüsselt oder entschlüsselt werden kann muß eine Schlüsselzentrale für jeden Teilnehmer einen privaten und einen öffentlichen Schlüssel festlegen. Der private Schlüssel ist eine ganze positive Zahl d, der öffentliche Schlüssel besteht aus zwei ganzen positiven Zahlen e und n. Um diese Zahlen festzulegen, wählt die Schlüsselzentrale für jeden Teilnehmer zufällig zwei große Primzahlen p und q und bildet deren Produkt n=p*q. Damit hat sie den ersten Bestandteil des öffentlichen Schlüssels. Als e, den zweiten Bestandteil, legt sie eine Zahl fest, welche mit der Zahl (p-1)(q-1) keinen gemeinsamen Teiler hat. Der private Schlüssel d muß folgende Bedingung erfüllen: (e*d) mod [(p –1)(q-1)] = 1. Die Berechnung von d aus dieser Gleichung, bei der e, p und q bekannt sind erfolgt nach dem erweiterten euklidischen Algorithmus, der hier nicht näher beschrieben werden soll. Dem Teilnehmer wird nun die Zahl d geheim als privater Schlüssel mitgeteilt. Die Zahlen n und e werden mit seinem Namen veröffentlicht. Die Schlüsselzentrale sollte nun die Zahlen p und q vernichten, damit niemand mit ihrer Hilfe den geheimen Schlüssel bestimmen kann. Nun kann jeder mit dem öffentlichen Schlüssel verschlüsselte Mitteilungen an den Teilnehmer senden. Diese müssen im Klartext aus Zahlen bestehen, die nicht größer sind als n. Der Sender verschlüsselt den Klartext m nach der Formel c=m^e mod n, wobei c der Geheimtext, n und e der öffentliche Schlüssel ist. Der Empfänger entschlüsselt diese Nachricht nach der Formel m=c^d mod n, wobei d der geheime Schüssel ist. Dass das funktioniert, soll an einem einfachen Beispiel dargestellt werden.

Primzahlen: p = 47; q = 71

Öffentlicher Schlüssel: n = p*q -> n = 47 * 71 = 3337

e zufällig gewählt e = 79 = teilerfremd zu (p-1)(q-1) -> 46*70 = 3220

Privater Schlüssel: d=1019 (mit erweitertem euklidischen Algorithmus berechnet)

p und q werden nicht mehr benötigt, dürfen aber niemals bekanntgegeben werden.

Verschlüsselung

Die Nachricht M = 688232687966668 wird in Blöcke unterteilt, so dass m nicht größer werden kann als n.

m₁= 688; m₂= 232; m₃= 687; m₄= 966; m₅= 668

c_i = m_i^e mod n

c₁= 688⁷⁹ mod 3337 = 1570

C = c₁+ c₂+...+c_n C = 1570 2756 2096 2276 2423

Entschlüsselung

m_i = c_i^d mod n

m₁= 1570¹⁰¹⁹ mod 3337 = 688

Sicherheit von RSA

Die Sicherheit von RSA beruht auf dem Problem der Faktorisierung großer Zahlen. Liegen p und q in der Größenordnung von 100 - 200 Stellen, so hat n 200 – 400 Stellen (Wir erinnern uns: n=p*q). Die nächstliegende Angriffsmethode ist also die Faktorisierung von n, da mit dem öffentlichen Schlüssel n und e bekannt sind. Um also den privaten Schlüssel d zu berechnen muß man n faktorisieren. Zum heutigen Zeitpunkt nimmt man an, dass Zahlen bis 129 Stellen in endlicher Zeit zu faktorisieren sind, so dass man mit der Wahl von n deutlich größer als 129 Stellen auf der sicheren Seite ist. Ein weiterer möglicher Angriff wäre die „Brute Force“-Methode. Dabei wird jedes mögliche d probiert, bis man den richtigen Wert gefunden hat. Dies ist bei RSA allerdings noch ineffizienter als eine Faktorisierung von n, weil der Schlüsselvorrat so groß ist, dass systematisches Durchprobieren unmöglich ist. Damit wäre ein minimales Sicherheitskriterium erfüllt. RSA wurde durch seine Veröffentlichung gut untersucht, aber trotzdem als solcher nicht geknackt. Sein Schwachpunkt liegt einzig und allein in der Faktorisierung großer Zahlen. Er ist damit praktisch sicher, obgleich er theoretisch angreifbar ist. Sobald eine Möglichkeit gefunden wird, mehrere hundert Bit lange Zahlen zu faktorisieren, ist der RSA- Algorithmus praktisch wertlos.

5 Integrität und Authentizität

5.0 Einordnung

Alle bisherigen Verfahren beschäftigten sich damit, die zu übermittelnden Nachrichten gegen unberechtigtes Mitlesen, also gegen passive Angriffe zu schützen. Wie kann man aber sicher sein, dass eine Nachricht unverändert beim Empfänger ankommt, die Integrität der Nachricht also gewährleistet ist? Wenn man davon ausgeht, dass der Übertragungsweg unsicher ist, so muß man sich Möglichkeiten schaffen, die Unversehrtheit von Nachrichten prüfen zu können. Daran schließt sich das Problem der Identität des Senders an, d. h. der Empfänger braucht Mittel um sich davon zu überzeugen, dass sein Kommunikationspartner auch der ist, für den er sich ausgibt. Man spricht hier von Authentikation.

5.1 Integrität von Nachrichten

Im folgenden wird ein mögliches Verfahren erläutert, mit dessen Hilfe man überprüfen kann, ob die übermittelte Nachricht verfälscht oder verändert wurde.

Der kryptographische Fingerabdruck

Mittels eines geheimen Schlüssels k, den beide Kommunikationspartner besitzen wird aus der Nachricht nach einem bestimmten Algorithmus (z.B. Cipher-Block-Chaining-Mode) eine Prüfsumme MAC (message authentication code) berechnet und zusammen mit der Nachricht übermittelt. Der Empfänger kann nun seinerseits diese Prüfsumme berechnen und bei Übereinstimmung sicher sein, dass die Nachricht nicht verändert wurde.

Cipher - Block - Chaining - Mode

[siehe Anlage 6]

• Klartext wird in Blöcke gleicher Länge eingeteilt (typisch sind 64 Bit) m₁, m₂, ..., m_n

• Bearbeitung von Block 1 mit Hilfe des Schlüssels k: c₁ = f_k (m₁)

• Block m₂ wird mit c₁ EXOR verknüpft (binäre Addition ohne Übertrag)

• c₂ = f_k ( c₁+m₂ )

• c₃ = f_k ( c₂+m₃ ) usw.

• der letzte verschlüsselte Block wird als MAC genommen

• c_n= f_k ( c_n-1+m_n )

Der Vorteil dieses Verfahrens ist, dass die Prüfsumme MAC eine feste Länge unabhängig von der Länge des Klartextes hat, aber trotzdem alle Blöcke in die Berechnung mit eingehen. Die Funktion f_k kann ein symmetrisches oder asymmetrisches Verschlüsselungsverfahren sein, wobei letzteres auf jeden Fall vorzuziehen ist, da kein geheimer Schlüsselaustausch zwischen den Kommunikationspartnern notwendig ist. Der Sender bildet die MAC dabei mit Hilfe seines privaten Schlüssels und jeder Empfänger kann die Echtheit mit dem öffentlichen Schlüssel des Senders überprüfen.

5.2 Benutzerauthentikation

Eine Grundaufgabe der Sicherheitstechnik ist es, die Identität von Personen sicherzustellen, d.h. sie zu authentifizieren. Personen können z.B. durch Kenntnis eines Passworts oder durch den Besitz eines Schlüssels oder einer Zugangskarte authentifiziert werden.

Passwörter

Passwörter ohne Verschlüsselung sind sinnlos, da jeder, der über das entsprechende know-how verfügt diese einfach auslesen könnte. Deshalb werden die Passwörter P₀ mit Einwegfunktionen verschlüsselt P*=f(P₀) und nur das verschlüsselte Ergebnis auf dem Rechner gespeichert. Einwegfunktionen sind mathematische Funktionen, die sich ohne großen Aufwand berechnen lassen, deren Umkehrfunktionen aber praktisch unbestimmbar sind. Gibt nun der Benutzer ein Passwort ein wird es mittels dieser Funktion verschlüsselt und das Ergebnis mit dem gespeicherten P* verglichen. Sind die beiden verschlüsselten Passwörter identisch hat sich der Benutzer erfolgreich authentifiziert.

Challenge and Response Verfahren

• Verwendung bei Chipkarten

• die ausgetauschten Daten ändern sich ständig

• Ziel: indirektes Überzeugen ob Benutzer im Schlüsselbesitz ist

Beispiel zwischen Chipkarte und Rechner

• beider verfügen über geheimen Schlüssel k

• Rechner schickt Zufallszahl RAND an Chipkarte

• Chipkarte verschlüsselt RAND mit k

• Antwort ANTW = f_k ( RAND )

• Rechner vergleicht ANTW == f_k ( RAND ) ?

• Vorteil: Es werden nur Zufallszahlen ausgetauscht.

5.3 Zero- Knowledge- Protokolle

Grundgedanke dieser Protokolle ist, jemanden davon zu überzeugen, dass man im Besitz eines Geheimnisses (Schlüssels) ist, ohne davon das Geringste zu verraten.

Das Fiat -Shamir -Protokoll

• aufgestellt 1986 durch Adi Shamir und Amos Fiat

• beruht auf der Schwierigkeit die modulare Quadratwurzel einer Zahl v zu finden

• s² MOD n = v

• praktisch unmöglich die Zahl s zu finden

Aufgabe der Schlüsselzentrale:

• zwei Primzahlen p und q werden multipliziert n=p*q

• p, q sind geheim, n ist öffentliche Systemkonstante

• s wird zufällig gewählt und daraus v jedes Benutzers berechnet v=s² mod n

• v dient der öffentlichen Identifizierung des Benutzers, s ist der geheime Schlüssel

• die Schlüsselzentrale spielt im Authentikationsprozess keine Rolle

Der Ablauf der Authentikation ist im Ablaufschema [siehe Anlage 3] dargestellt. Der Verifizierer wird irgendwann davon überzeugt sein, dass der Benutzer das Geheimnis s besitzt. Die Wahrscheinlichkeit für die Vorhersage des Bits b ist bei t-maliger Ausführung 0,5^t. Nach 20 Durchläufen ist die Wahrscheinlichkeit kleiner als 1 zu einer Million. Auch nach dem Authentikationsprozess bleibt das Geheimnis s absolut geheim.

6 Anwendungen

6.0 Motivation

Am Anfang hatten wir die These aufgestellt, jeder in unserer heutigen Gesellschaft hat mit Kryptologie in irgendeiner Art und Weise zu tun. Bisher haben wir die zeitliche Entwicklung der Kryptologie dargestellt und einen groben Überblick über die wichtigsten Verfahren gegeben. Vielleicht wurde an der einen oder anderen Stelle bewußt, warum die Anwendung kryptologischer Verfahren so bedeutungsvoll in dieser Zeit ist. Wir haben mehrere Umbrüche in der Entwicklung unserer Gesellschaft hinter uns. Angefangen mit der auf Landwirtschaft basierenden Zivilisation, über Handwerk bis hin zur industriellen Revolution bewegen wir uns heute im Zeitalter der Information. Dass Wissen Macht ist, wird dann deutlich, wenn Firmen Neuentwicklungen vor der Konkurrenz schützen wollen, wenn bestimmte Datenbanken nur gegen Entgelt durchforstbar sind, wenn Politiker peinlich-beschämende Vorgänge nicht veröffentlichen wollen. Aber auch deine Privatsphäre und Sicherheit können gefährdet sein! Umfangreiche Banken-, Kreditkarten- und medizinische Daten, eMail-Überwachung und Computerschnüffelprogramme sind nur einige wenige Faktoren, die jeden gesetzestreuen Bürger treffen. Kurz gesagt, unsere in Privatsachen schnüffelnde Gesellschaft dient den Kriminellen und serviert persönliche Daten auf einem Silbertablett. Im allgemeinen gilt, dass klassische Sicherheitsaspekte der Integrität, Vertraulichkeit, Verfügbarkeit, Verbindlichkeit und Authentizität zunehmend allgemein gewünschte Merkmale von Kommunikationsprozessen sind. Sichere Kommunikation ist Voraussetzung für wirtschaftliche und behördliche Netzteilnahme. An dieser Stelle soll ein Überblick über die Anwendung kryptologischer Verfahren in der Praxis gegeben werden.

6.1 PGP und GnuPG

Was ist PGP?

PGP - ausgeschrieben "Pretty Good Privacy" (ziemlich gute Privatsphäre) - ist ein Computerprogramm, das Daten verschlüsselt und entschlüsselt. Philip Zimmermann schrieb das erste Programm. Phil - ein Held für viele Unterstützer des Datenschutzes - arbeitet als Sicherheitsexperte in Boulder, Colorado. Andere Programmierer aus der ganzen Welt haben an den nachfolgenden PGP Versionen und Benutzungsoberflächen mitgeholfen. PGP benutzt das RSA Public-Key Verschlüsselungssystem und ein Verschlüsselungssystem namens IDEA welches 1990 von Xuejia Lai und James Massey entwickelt wurde.

Was ist GnuPG?

GnuPG ist eine von Werner Koch aus Düsseldorf entwickelte Verschlüsselungs-Software. GnuPG wird von Sicherheitsexperten in aller Welt als eines der derzeit besten Verschlüsselungssysteme anerkannt. Das Besondere an GnuPG:

• GnuPG implementiert den OpenPGP-Standard, der als Erweiterung von PGP den derzeitigen de-facto-Standard im Internet darstellt.

• GnuPG ist ein offizielles GNU-Projekt und freie Software unter der GNU General Public License (GNU GPL).

Wie arbeiten PGP und GnuPG?

PGP und GnuPG sind "öffentliche Schlüsselsysteme" (public key cryptography). Wenn man PGP bzw. GnuPG das erste Mal startet, generiert es zwei "Schlüssel". Ein PGP-Schlüssel ist der geheime Schlüssel und bleibt auf dem Rechner. Der andere Schlüssel ist öffentlich und wird den Gesprächspartnern übergeben, die ihn in ihrem PGP-Programm speichern. Will Person A an Person B eine Nachricht schreiben benutzt, sie zur Verschlüsselung den öffentlichen Schlüssel von B. Nur Person B kann diese Nachricht mit ihrem geheimen Schlüssel wieder dechiffrieren.

Wie sicher ist PGP bzw. GnuPG?

Hervorragende Kryptoanalytiker und Computerexperten haben vergeblich versucht, PGP zu knacken. Wer auch immer nachweist, dass er PGP enträtselt hat, wird schnell zu Ruhm unter den Kryptographen kommen. Er wird viel Beifall ernten und eine Menge Geld angeboten bekommen. Die PGP Programmierer werden dies sofort bekanntgeben. Fast täglich verbreitet jemand eine Nachricht, wie "PGP durch Jugendlichen aus Omaha geknackt". Bis heute hat niemand öffentlich vorgeführt, PGP überlistet oder geknackt zu haben.

6.2 SSH (Secure Shell)

Alles, was ein Rechner ins Netz schickt, kann prinzipiell von allen anderen Rechnern im gleichen Netzsegment gelesen werden. Daher muß man sich bei der Benutzung von Netzdiensten Gedanken machen, welche Gefahren die Abhörbarkeit mit sich bringt. Besonders kritisch in dieser Hinsicht sind jede Art von Passwörtern: wer sich in den Besitz eines gültigen Accountname/Passwort-Paars bringt, kann damit auf fremden Rechnern beliebigen Unfug treiben. Ein normales Telnet, FTP mit Passwort und andere Dienste übertragen immer Passwörter im Klartext und stellen damit ein Risiko dar. Es sollte das Ziel sein, niemals Passwörter im Klartext zu senden. Alle Netzdienste, die eine Benutzeridentifikation mit Passwort benötigen, sollten nur über eine SSH-Verbindung benutzt werden.

Authentifizierungsverfahren

SSH bietet mehrere Möglichkeiten, wie sich der Benutzer dem Server gegenüber authentifiziert. Relevant sind insbesondere die Methoden "PasswordAuthentication" und "RSAAuthentication". Das Passwortverfahren wird dann verwendet, wenn eine Authentifizierung mit anderen Methoden nicht möglich ist. Dabei fragt der SSH-Client das Userpasswort in konventioneller Weise ab, schickt es aber verschlüsselt zum Server. Der Server wiederum behandelt das Passwort in der gewohnten Weise. Damit ist das Verfahren genauso zu handhaben wie Telnet, aber sicherer, da kein Abhören möglich ist. Wirklich interessant ist die RSA-Authentifizierung. Dabei wird der RSA-Public-Key-Algorithmus verwendet. Der Benutzer besitzt einen geheimen Schlüssel und der Host, auf dem er sich einloggen will (Zielhost) den dazugehörigen öffentlichen Schlüssel. Wie bei der Verifikation einer PGP-Signatur kann der Server feststellen, ob der geheime Schlüssel stimmt, ohne dass direkt brauchbare Klartextdaten übertragen werden.

TCP-Portumlenkung

Gleichzeitig mit der Login-Funktion arbeitet SSH auch als TCP-Proxy. Beim Aufruf des SSH-Befehls kann man beliebig angeben, dass TCP-Verbindungen auf bestimmten Ports der einen Seite auf Verbindungen auf der anderen Seite umgelenkt werden sollen. Dabei kommt zwischen beiden wiederum ein verschlüsselter Kanal zum Einsatz.

POP

Mail mit POP zu verarbeiten, ist bequem und daher recht beliebt (und in den Standard-Mailprogrammen mancher Systeme eingebaut), stellt aber ein erhebliches Sicherheitsproblem dar. POP verlangt die Angabe des eigenen Account-Passwortes, das im Klartext übertragen wird. POP arbeitet auf einer einzelnen TCP-Verbindung zu einem bekannten Port und ist dadurch sehr einfach mit SSH zu sichern, so dass dieses Problem nicht mehr auftritt.

6.3 Chipkarten

Chipkarten gewinnen zunehmend an gesellschaftlicher Bedeutung, die derzeit bekannteste Chipkarten-Anwendung ist die Telefonkarte. Weitere Anwendungsbereiche von Chipkarten sind z. B. die Chipkarte im bargeldlosen Zahlungsverkehr und die SIM-Karten in Handys. Sie erfüllen dabei folgende Aufgaben:

• Speicher von Daten, die hinsichtlich ihrer Vertraulichkeit und/oder Integrität hohen Schutzbedarf aufweisen (z. B. Kontodaten, medizinische Individualdaten, Personalausweisdaten, Führerscheindaten)

• Mittel zur Authentisierung ihres Trägers für die Gewährung des Zugriffs auf sicherheitsrelevante Daten und Funktionen (Kontoverfügungen, Führen von Telefongesprächen über Mobilfunknetze)

• Mittel zur Signatur von Dokumenten (Verträge, Willenserklärungen, Befunde etc.)

• Träger elektronischer Geldbörsen.

Um diesen Anforderungen gerecht zu werden verfügen Chipkarten über Sicherheitstechnologien, die den Schutz der Daten vor Mißbrauch gewährleisten sollen. Die Schutzfunktionen der Chipkarten-Software basieren auf den bekannten und teilweise standardisierten Algorithmen zur Verschlüsselung, Signatur und Generierung von Zufallszahlen. Dazu gehören symmetrische Verschlüsselungsalgorithmen wie DES, Triple-DES, IDEA und SC85 und asymmetrische Verfahren wie RSA, Signieralgorithmen wie DSS und RSA mit RipeMD160, Einwegfunktionen zur Berechnung des MAC und für das Hashing wie SHA und RipeMD160 sowie Zufallszahlengeneratoren. Für detailliertere Informationen sei hier auf die Quelle [CHPCRD] verwiesen.

Anlagen

Anlage 1

Tabelle 9: Vigenère-Quadrat

a b c d e f g h i j k l m n o p q r s t u v w x y z
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
B C D E F G H I J K L M N O P Q R S T U V W X Y Z A
C D E F G H I J K L M N O P Q R S T U V W X Y Z A B
D E F G H I J K L M N O P Q R S T U V W X Y Z A B C
E F G H I J K L M N O P Q R S T U V W X Y Z A B C D
F G H I J K L M N O P Q R S T U V W X Y Z A B C D E
G H I J K L M N O P Q R S T U V W X Y Z A B C D E F
H I J K L M N O P Q R S T U V W X Y Z A B C D E F G
I J K L M N O P Q R S T U V W X Y Z A B C D E F G H
J K L M N O P Q R S T U V W X Y Z A B C D E F G H I
K L M N O P Q R S T U V W X Y Z A B C D E F G H I J
L M N O P Q R S T U V W X Y Z A B C D E F G H I J K
M N O P Q R S T U V W X Y Z A B C D E F G H I J K L
N O P Q R S T U V W X Y Z A B C D E F G H I J K L M
O P Q R S T U V W X Y Z A B C D E F G H I J K L M N
P Q R S T U V W X Y Z A B C D E F G H I J K L M N O
Q R S T U V W X Y Z A B C D E F G H I J K L M N O P
R S T U V W X Y Z A B C D E F G H I J K L M N O P Q
S T U V W X Y Z A B C D E F G H I J K L M N O P Q R
T U V W X Y Z A B C D E F G H I J K L M N O P Q R S
U V W X Y Z A B C D E F G H I J K L M N O P Q R S T
V W X Y Z A B C D E F G H I J K L M N O P Q R S T U
W X Y Z A B C D E F G H I J K L M N O P Q R S T U V
X Y Z A B C D E F G H I J K L M N O P Q R S T U V W
Y Z A B C D E F G H I J K L M N O P Q R S T U V W X
Z A B C D E F C H I J K L M N O P Q R S T U V W X Y

Anlage 2

Tabelle 10: Kasiski-Test

Anlage 3

Tabelle 11: Fiat-Shamir-Protokoll

Anlage 4

Bild 1: Ablauf des DES-Algorithmus

Anlage 5

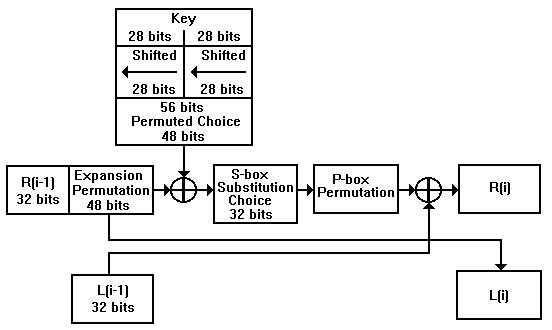
Bild 2: Auflauf einer Runde des DES-Algorithmus

Anlage 6

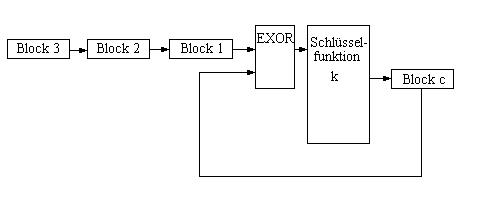
Bild 3: Cipher-Block-Chaining-Mode

Quellennachweis